Câu hỏi
Một sóng hình sin lan truyền trên phương Ox với tân số 10 Hz. Tại thời điểm t1 hai phần tử M và N gần nhau nhất có cùng li độ tương ứng là -1,6cm và 1,6cm. Tại thời điểm t2 gần t1nhất thì li độ của M và N đều bằng nhau và bằng 1,2cm. Tốc độ cực đại của các phần tử trên phương truyền sóng gần nhất với giá trị nào sau đây ?
- A 130 cm/s.
- B 100 cm/s.
- C 116 cm/s.
- D 124 cm/s.
Phương pháp giải:
Sử dụng VTLG và tìm được biên độ A.
Tốc độ cực đại: \({v_{\max }} = \omega A = 2\pi fA\)
Lời giải chi tiết:
Ban đầu M và N có li độ -1,6 cm và 1,6 cm, ta có ĐTLG
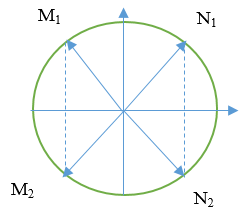
Vì M và N là là hai phần tử gần nhau nhất, nên từ hình vẽ, ta lấy đó là điểm M1 và N1
Khi M và N có li độ 1,2 cm, ta có ĐTLG
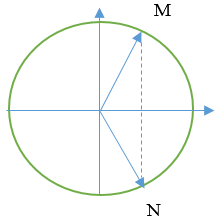
Vậy từ t1 đến t2góc quét của hai vecto \(\overrightarrow {OM} \) và \(\overrightarrow {ON} \) như nhau.
Ta có:
\(\arcsin \frac{{1,6}}{A} + \arcsin \frac{{1,2}}{A} = {\rm{arccos}}\frac{{1,6}}{A} + \arccos \frac{{1,2}}{A}\)
Bấm máy tính và tìm được A = 2cm
Tốc độ cực đại của các phần tử là:
\(v = \omega A = 2\pi fA = 40\pi \approx 124\left( {cm/s} \right)\)
Chọn D.







