Câu hỏi
Một con lắc đơn gồm vật có khối lượng m, dây treo có chiều dài l = 2 m, lấy g = π2 m/s2. Con lắc dao động điều hòa dưới tác dụng của ngoại lực có biểu thức \(F = {F_0}\cos \left( {\omega t + \dfrac{\pi }{2}} \right)\,\,\left( N \right)\). Nếu chu kỳ T của ngoại lực tăng từ 2 s lên 4 s thì biên độ dao động của vật sẽ
- A tăng rồi giảm.
- B chỉ tăng.
- C chỉ giảm.
- D giảm rồi tăng.
Phương pháp giải:
Tần số dao động riêng của con lắc: \(T = 2\pi \sqrt {\dfrac{l}{g}} \)
Biên độ dao động của con lắc lớn nhất khi xảy ra cộng hưởng, tần số góc của ngoại lực: \(\omega = \Omega \)
Lời giải chi tiết:
Chu kì dao động riêng của con lắc là:
\({T_0} = 2\pi \sqrt {\dfrac{l}{g}} = 2\pi \sqrt {\dfrac{2}{{{\pi ^2}}}} = 2\sqrt 2 \approx 2,83\,\,\left( s \right)\)
Ta thấy \(2 < {T_0} < 4 \to \) chu kì tăng từ \(2\,\,s\) lên \(4\,\,s\), có giá trị để con lắc cộng hưởng.
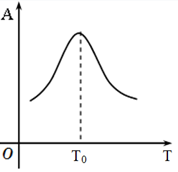
Vậy biên độ của con lắc tăng rồi giảm
Chọn A.







