Phương pháp giải:

- Xác định khoảng cách từ O đến \(\left( P \right)\).

- Sử dụng định lí Pytago và hệ thức lượng trong tam giác vuông tính chiều cao và đáy của tam giác thiết diện.

Lời giải chi tiết:

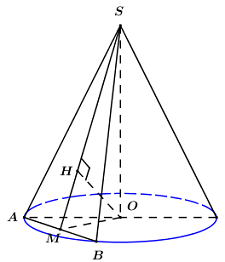
Giả sử \(\left( P \right)\) cắt hình nón theo thiết diện là \(\Delta SAB\) cân tại \(S\).

Gọi \(O\) là tâm mặt đáy, \(M\) là trung điểm của \(AB\) ta có:

\(\left\{ \begin{array}{l}AB \bot OM\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOM} \right)\).

Trong \(\left( {SOM} \right)\) kẻ \(OH \bot SM\) ta có \(\left\{ \begin{array}{l}OH \bot SM\\OH \bot AB\end{array} \right. \Rightarrow OH \bot \left( {SAB} \right)\) hay \(OH \bot \left( P \right)\) \( \Rightarrow d\left( {O;\left( P \right)} \right) = OH = a\).

Áp dụng hệ thức lượng trong tam giác vuông SOM có:

\(\begin{array}{l}\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{M^2}}}\\ \Leftrightarrow \dfrac{1}{{{a^2}}} = \dfrac{1}{{2{a^2}}} + \dfrac{1}{{O{M^2}}}\\ \Rightarrow \dfrac{1}{{O{M^2}}} = \dfrac{1}{{2{a^2}}} \Rightarrow OM = a\sqrt 2 \end{array}\)

Áp dụng định lí Pytago ta có:

\(\begin{array}{l}AM = \sqrt {O{A^2} - O{M^2}}  = \sqrt {4{a^2} - 2{a^2}}  = a\sqrt 2 \\ \Rightarrow AB = 2AM = 2a\sqrt 2 \\SM = \sqrt {S{O^2} + O{M^2}}  = \sqrt {2{a^2} + 2{a^2}}  = 2a\end{array}\)

Vậy

\({S_{\Delta SAB}} = \dfrac{1}{2}SM.AB = \dfrac{1}{2}.2a.2a\sqrt 2  = 2\sqrt 2 {a^2}\).

Chọn D.