Câu hỏi
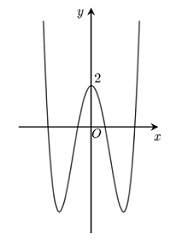
Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây.
Hàm số đó là hàm số nào?
- A \(y = {x^4} - 5{x^2} + 2\).
- B \(y = {x^3} + 3{x^2} + 2\).
- C \(y = - {x^4} + 5{x^2} + 2\).
- D \(y = {x^4} + 5{x^2} + 2\).
Phương pháp giải:
- Dựa vào số điểm cực trị của hàm số xác định đó là hàm đa thức bậc ba hay bậc bốn trùng phương.
- Dựa vào \(\mathop {\lim }\limits_{x \to + \infty } y\) xác định dấu của hệ số a.
- Hàm đa thức bậc bốn trùng phương \(y = a{x^4} + b{x^2} + c\) có 3 điểm cực trị \( \Leftrightarrow ab < 0\).
Lời giải chi tiết:
Quan sát đồ thị hàm số, ta thấy: Hàm số có 3 điểm cực trị nên đây không phải đồ thị hàm số bậc ba, nên loại phương án B.
Khi đó, đây chỉ có thể là đồ thị của hàm số bậc 4 trùng phương (các phương án còn lại : A, C, D) dạng: \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\).
Ta thấy \(\mathop {\lim }\limits_{x \to + \infty } y = + \infty \) \( \Rightarrow a > 0 \Rightarrow \) Loại phương án C.
Đồ thị hàm số có ba điểm cực trị \( \Rightarrow ab < 0\), mà \(a > 0\) \( \Rightarrow b < 0 \Rightarrow \) Loại phương án D. Chọn phương án A.
Chọn A.







