Phương pháp giải:

+ Sử dụng công thức lượng giác

+ Sử dụng biểu thức: \(\tan \left( {a - b} \right) = \dfrac{{{\rm{tana - tanb}}}}{{1 + \tan a.\tan b}}\)

+ Sử dụng biểu thức tính độ lệch pha: \(\Delta \varphi  = \dfrac{{2\pi d}}{\lambda }\)

+ Điều kiện ngược pha: \(\Delta \varphi  = \left( {2k + 1} \right)\pi \)

Lời giải chi tiết:

Ta có, giữa A và B có 5 đỉnh sóng với A, B cũng là đỉnh sóng

\( \Rightarrow AB = 4\lambda \)

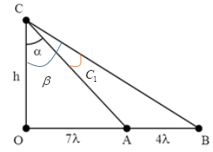
Ta có: \(\left\{ \begin{array}{l}\tan \alpha  = \dfrac{{7\lambda }}{h}\\\tan \beta  = \dfrac{{7\lambda  + 4\lambda }}{h} = \dfrac{{11\lambda }}{h}\end{array} \right.\)

Ta có: \(\beta  - \alpha  = {C_1}\)

\( \Rightarrow \tan \left( {\beta  - \alpha } \right) = \dfrac{{\tan \beta  - \tan \alpha }}{{1 + \tan \beta \tan \alpha }} = \dfrac{{\dfrac{{11\lambda }}{h} - \dfrac{{7\lambda }}{h}}}{{1 + \dfrac{{11\lambda }}{h}.\dfrac{{7\lambda }}{h}}} = \dfrac{{4\lambda }}{{h + \dfrac{{77{\lambda ^2}}}{h}}}\)

Từ biểu thức trên, ta thấy \({C_1} = \widehat {ACB}\) lớn nhất khi mẫu nhỏ nhất

Có \(h + \dfrac{{77{\lambda ^2}}}{h} \ge 2\sqrt {77{\lambda ^2}} \)

Dấu “=” xảy ra khi \(h = \sqrt {77} \lambda \)

+ Gọi M là một điểm trên AC, để M dao động ngược pha với nguồn thì \(\Delta {\varphi _M} = \dfrac{{2\pi {d_M}}}{\lambda } = \left( {2k + 1} \right)\pi \)

\( \Rightarrow {d_M} = \left( {2k + 1} \right)\dfrac{\lambda }{2}\)

+ Xét khoảng giá trị của M, tính về phía C từ đường vuông góc của O lên AC, ta có:

\(5,47\lambda  \le {d_M} \le 8,7\lambda \)

Sử dụng chức năng TABLE trong máy tính ta tìm được 4 vị trí

 + Xét đoạn về phía A: \(5,47\lambda  \le {d_M} \le 7\lambda \)

Cũng sử dụng chức năng TABLE trong máy tính ta tìm được 2 vị trí

Vậy trên AC có 6 vị trí

Chọn C