Câu hỏi
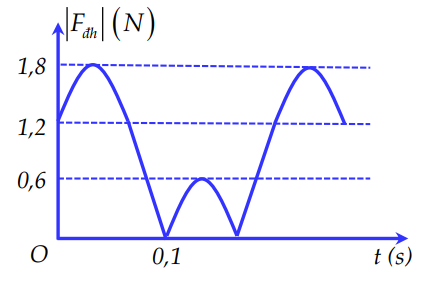
Một con lắc lò xo treo thẳng đứng đang dao động điều hòa. Hình bên là đồ thị mô tả sự phụ thuộc giữa độ lớn lực đàn hồi của lò xo theo thời gian t. Lấy g = π2 m/s2. Mốc thế năng tại vị trí cân bằng. Cơ năng của con lắc là:
- A 15 mJ
- B 18 mJ
- C 9 mJ
- D 12 mJ
Phương pháp giải:
Từ đồ thị ta thấy Fdhmax = 1,8N; Fmin = 0; sau đó Fdh tăng đến 0,6N rồi giảm; vậy lò xo có biên độ A lớn hơn độ dãn ∆l0
Áp dụng công thức lực đàn hồi
\(F = k.\left( {x + \Delta {l_0}} \right)\)
Vị trí khi t = 0 đến t = 0,1s thì F = 0, tức là vật ở vị trí lò xo không dãn.
Ta sử dụng VTLG tìm chu kì, tần số góc.
Áp dụng công thức tính năng lượng:
\({\rm{W}} = \frac{1}{2}.k.{A^2}\)
Lời giải chi tiết:
+ Từ đồ thị ta thấy Fdhmax = 1,8N; Fmin = 0; sau đó Fdh tăng đến 0,6 N rồi giảm; vậy lò xo có biên độ A lớn hơn độ dãn ∆l0
+ Áp dụng công thức lực đàn hồi :
\(\left\{ \begin{array}{l}
{F_{dh\max }} = k.\left( {A + \Delta {l_0}} \right) = 1,8\\
{F_{dh\min }} = k.\left( {A - \Delta {l_0}} \right) = 0,6
\end{array} \right.\)
\(\begin{array}{l}
\Rightarrow \frac{{{F_{dh\max }}}}{{{F_{dh\min }}}} = \frac{{A + \Delta {l_0}}}{{A - \Delta {l_0}}} = 3 \Rightarrow \Delta {l_0} = \frac{A}{2}\\
\Rightarrow {F_{dh\max }} = k.\left( {A + \frac{A}{2}} \right) = 1,8 \Leftrightarrow k.A = 1,2
\end{array}\)
+ Vị trí khi t = 0 thì F = 1,2N, vậy vật đang ở vị trí dãn một đoạn bằng A, tức là có tọa độ
Đến t = 0,1s thì F = 0, tức là vật ở vị trí lò xo không dãn.
+ Ta có VTLG:
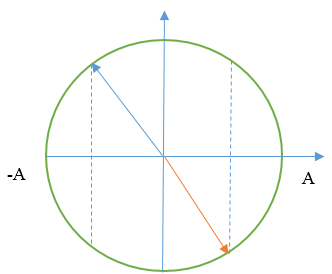
Vậy chu kì:
\(T = 2.0,1 = 0,2s \Rightarrow \omega = \frac{{2\pi }}{T} = 10\pi \left( {rad/s} \right)\)
Mà \(\omega = \sqrt {\frac{g}{{\Delta {l_0}}}} = 10\pi \Rightarrow \Delta {l_0} = 0,01m = 1cm\)
Nên \(A = 2.\Delta {l_0} = 0,02m\)
Ta có năng lượng của dao động là:
\({\rm{W}} = \frac{1}{2}.k.{A^2} = \frac{1}{2}.k.A.A = \frac{1}{2}.1,2.0,02 = 0,012J = 12mJ\)
Chọn D.







