Câu hỏi
Tại thời điểm đầu tiên t = 0 đầu O của sợi dây cao su căng thẳng nằm ngang bắt đầu dao động đi lên với tần số 2 Hz với biên độ \(A = 6\sqrt 5 cm\). Gọi P, Q là hai điểm cùng nằm trên một phương truyền sóng cách O lần lượt là 6 cm và 9 cm. Biết vận tốc truyền sóng trên dây là 24 cm/s và coi biên độ sóng không đối khi truyền đi. Tại thời điểm O, P, Q thẳng hàng lần thứ 2 thì vận tốc dao động của điểm P và điểm Q lần lượt là vP và vQ. Chọn phương án đúng
- A vQ = 24π cm/s.
- B vP = 48π cm/s.
- C vQ = −24π cm/s.
- D vP = −24π cm/s.
Phương pháp giải:
Bước sóng: \(\lambda = \frac{v}{f}\)
Công thức tính độ lệch pha: \(\Delta \varphi = \frac{{2\pi d}}{\lambda }\)
Phương trình sóng: \(u = A.cos\left( {\omega t + \varphi } \right)\)
Phương trình vận tốc của phần tử sóng: v= u'
Lời giải chi tiết:
Bước sóng: \(\lambda = \frac{v}{f} = \frac{{24}}{2} = 12cm\)
Sử dụng công thức tính độ lệch pha:
\(\Delta \varphi = \frac{{2\pi d}}{\lambda }\), ta có:
+ P cách O nửa bước sóng do vậy P luôn ngược pha với O
+ Q cách O một khoảng 0,75λ nên Q luôn vuông pha với O.
+ Q cách P một phần tư bước sóng, do đó Q cũng vuông pha với P.
Ta có hình vẽ:
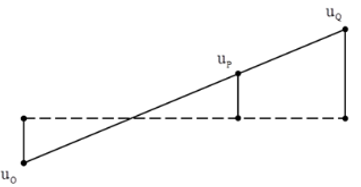
Từ hình vẽ, ta thấy rằng khi O,P,Q thẳng hàng thì:
\(\frac{{{u_Q}}}{{{u_P}}} = \frac{6}{3} = 2 \Rightarrow {u_Q} = 2{u_P}\)
Mặt khác P và Q luôn cùng pha nên ta có:
\(\left\{ \begin{array}{l}
\left| {{v_P}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_P}}}{A}} \right)}^2}} = 48{\pi _{}}cm/s\\
\left| {{v_Q}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_Q}}}{A}} \right)}^2}} = 24{\pi _{}}cm/s
\end{array} \right.\)
Tốc độ của điểm P và Q tương ứng là
\(\left\{ \begin{array}{l}
\left| {{v_P}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_P}}}{A}} \right)}^2}} = 48{\pi _{}}cm/s\\
\left| {{v_Q}} \right| = \omega A\sqrt {1 - {{\left( {\frac{{{u_Q}}}{A}} \right)}^2}} = 24{\pi _{}}cm/s
\end{array} \right.\)
Lần thẳng hàng thứ 2 ứng với \({v_Q} = 24\pi cm/s\)
Chọn B.







