Câu hỏi
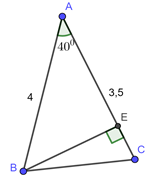
Cho tam giác \(ABC\)có \(AB = 4;AC = 3,5\). Tính diện tích tam giác \(ABC\) trong hai trường hợp:
Câu 1:
\(\angle A = {40^0}\)
- A \({S_{ABC}} = 4\,\,\left( {dvdt} \right)\)
- B \({S_{ABC}} = 4,5\,\,\,\left( {dvdt} \right)\)
- C \({S_{ABC}} = 4,8\,\,\,\left( {dvdt} \right)\)
- D \({S_{ABC}} = 5,2\,\,\,\left( {dvdt} \right)\)
Phương pháp giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông.
Công thức tính diện tích tam giác.
Lời giải chi tiết:
\(\angle A = {40^0}\)
Kẻ \(BE \bot AC,\,\,E \in AC.\)
Xét \(\Delta BEA\) vuông tại \(E\) ta có: \(BE = AB.sin\angle A = 4.sin{40^0}\)
\( \Rightarrow {S_{ABC}} = \frac{{BE.AC}}{2} = \frac{{4\sin {{40}^0}.3,5}}{2} \approx 4,5\,\,\,\left( {dvdt} \right).\)
Chọn B.
Câu 2:
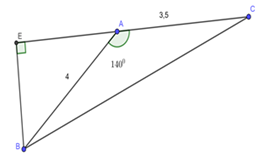
\(\angle A = {140^0}\)
- A \({S_{ABC}} = 4\,\,\left( {dvdt} \right)\)
- B \({S_{ABC}} = 4,5\,\,\,\left( {dvdt} \right)\)
- C \({S_{ABC}} = 4,8\,\,\,\left( {dvdt} \right)\)
- D \({S_{ABC}} = 5,2\,\,\,\left( {dvdt} \right)\)
Phương pháp giải:
Áp dụng hệ thức về cạnh và góc trong tam giác vuông
Sử dụng tính chất hai góc kề bù.
Công thức tính diện tích tam giác.
Lời giải chi tiết:
\(\angle A = {140^0}\)
Kẻ \(BE \bot AC\)
Xét \(\Delta BEA\) vuông tại \(E\) ta có:
Ta có: \(\angle BAE + \angle BAC = {180^0}\)
\( \Rightarrow \angle BAE = {180^0} - \angle BAC = {180^0} - {140^0} = {40^0}\)
Xét \(\Delta BEA\) vuông tại \(E\) ta có: \(BE = AB.sin\angle BAE = 4.sin{40^0}\)
\( \Rightarrow {S_{ABC}} = \frac{{BE.AC}}{2} = \frac{{4\sin {{40}^0}.3,5}}{2} \approx 4,5\,\,\,\left( {dvdt} \right).\)
Chọn B.