Câu hỏi
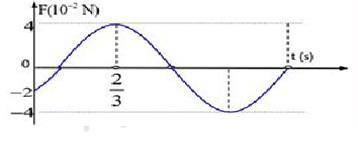
Một con lắc lò xo có vật nhỏ khối lượng 100 g dao động điều hòa theo phương nằm ngang hình 4 bên là đồ thị biểu diễn sự phụ thuộc của lực kéo về F theo thời gian t. Lấy π2= 10. Phương trình dao động của vật là
- A \(x = 4.\cos \left( {\pi t + \frac{\pi }{3}} \right)cm\)
- B \(x = 8.\cos \left( {2\pi t + \frac{\pi }{6}} \right)cm\)
- C \(x = 4.\cos \left( {\pi t - \frac{{2\pi }}{3}} \right)cm\)
- D \(x = 8.\cos \left( {2\pi t - \frac{\pi }{3}} \right)cm\)
Phương pháp giải:
Lực kéo về: \(F = - kx = - m.{\omega ^2}.A.\cos \left( {\omega t + \varphi } \right) = - {F_0}.\cos \left( {\omega t + \varphi } \right)\)
Lực kéo về cực đại: \({F_0} = kA\)
Áp dụng phương pháp vecto quay.
Lời giải chi tiết:
Tại thời điểm t = 0 thì:
\(\left\{ \begin{array}{l}
F = - 2N\\
{F_0} = 4N
\end{array} \right.\)
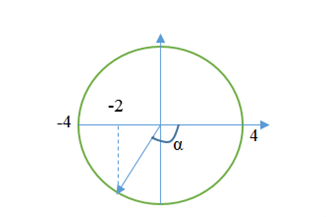
Ta có giản đồ vecto quay:
Ta có: \( - 2 = 4\cos \alpha \Rightarrow \cos \alpha = - \frac{1}{2} \Rightarrow \alpha = - \frac{{2\pi }}{3}\,\,\left( {rad} \right)\)
Nhận xét: lực kéo về ngược pha với li độ \( \to \) pha ban đầu của li độ là:
\({\varphi _x} = {\varphi _F} + \pi = - \frac{{2\pi }}{3} + \pi = \frac{\pi }{3}\,\,\left( {rad} \right)\)
Từ đồ thị, thời gian từ vị trí F = -2N đến F = 4N lần đầu tiên là \(\frac{2}{3}s\)
Ta có: \(t = \frac{\alpha }{{2\pi }}.T \Rightarrow \frac{2}{3}s = \frac{T}{3} \Rightarrow T = 2s \Rightarrow \omega = \frac{{2\pi }}{T} = \pi \,rad/s\)
Vậy: \(A = \frac{{{F_0}}}{{m.{\omega ^2}}} = \frac{{{{4.10}^{ - 2}}}}{{0,1.{\pi ^2}}} = {4.10^{ - 2}}\,\,\left( m \right) = 4\,\,\left( {cm} \right)\)
Vậy phương trình dao động là:
\(x = 4.\cos \left( {\pi t + \frac{\pi }{3}} \right)\)
Chọn A.