Câu hỏi
Cho đồ thị (C) của hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) như hình vẽ. Hãy xác định số diểm cực trị của hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\).
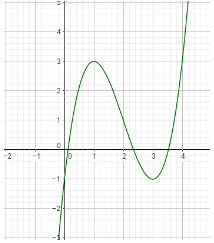
- A
2
- B 3
- C 4
- D 5
Phương pháp giải:
- Vẽ đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\):
+ B1: Vẽ đồ thị hàm số \(y = f\left( x \right)\).
+ B2: Xóa đi phần đồ thị hàm số \(y = f\left( x \right)\) nằm phía bên trái trục Oy.
+ B3: Lấy đối xứng phần đồ thị hàm số \(y = f\left( x \right)\) nằm phía dưới bên phải trục Oy qua trục Oy.
- Dựa vào đồ thị hàm số \(y = f\left( {\left| x \right|} \right)\) mới vẽ được xác định các điểm cực trị của hàm số (là điểm mà qua đó đồ thị hàm số đổi hướng từ đi lên thành đi xuống hoặc ngược lại).
Lời giải chi tiết:
Từ đồ thị hàm số \(y = {x^3} - 6{x^2} + 9x - 1\) ta suy ra được đồ thị hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) như sau (phần nét liền):
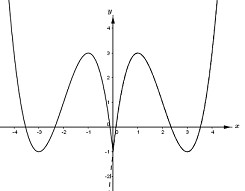
Dựa vào đồ thị hàm số ta thấy hàm số \(y = {\left| x \right|^3} - 6{x^2} + 9\left| x \right| - 1\) có 5 điểm cực trị.
Chọn D.







