Phương pháp giải:

- Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông.

Lời giải chi tiết:

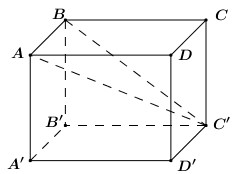
Ta có: \(\left\{ \begin{array}{l}AB \bot BC\\AB \bot BB'\end{array} \right. \Rightarrow AB \bot \left( {BCC'B'} \right)\), mà \(BC' \subset \left( {BCC'B'} \right)\) nên \(AB \bot BC'\).

Ta có: \(\left\{ \begin{array}{l}\left( {ABC'} \right) \cap \left( {ABCD} \right) = AB\\BC' \subset \left( {ABC'} \right),\,\,BC' \bot AB\\BC \subset \left( {ABCD} \right),\,\,BC \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {ABC';\left( {ABCD} \right)} \right) = \angle \left( {BC';BC} \right) = \angle CBC' = {60^0}\).

Xét tam giác vuông BCC’ có: \(CC' = BC.\tan {60^0} = a\sqrt 3 \).

Vậy cạnh bên của khối lăng trụ bằng \(a\sqrt 3 \).

Chọn A.