Câu hỏi
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh O, cạnh a, SA = a và vuông góc với đáy. Mặt phẳng \(\left( \alpha \right)\) đi qua O, trung điểm M của SD và vuông góc với đáy. Xác định thiết diện tạo bởi \(\left( \alpha \right)\) với hình chóp S.ABCD và tính diện tích thiết diện theo a.
Phương pháp giải:
Xác định các đường thẳng vuông góc với (ABCD), sử dụng tính chất đường trung bình của tam giác.
Chứng minh thiết diện là hình thang vuông. Sử dụng công thức tính diện tích hình thang.
Lời giải chi tiết:
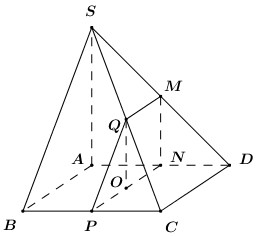
Gọi N và Q lần lượt là trung điểm của AD và SC.
Ta có:
MN là đường trung bình của tam giác SAD \( \Rightarrow MN\parallel SA\). Mà \(SA \bot \left( {ABCD} \right) \Rightarrow MN \bot \left( {ABCD} \right)\).
\( \Rightarrow MN \subset \left( \alpha \right)\).
OQ là đường trung bình của tam giác SAC \( \Rightarrow OQ\parallel SA\). Mà \(SA \bot \left( {ABCD} \right) \Rightarrow OQ \bot \left( {ABCD} \right)\).
\( \Rightarrow OQ \subset \left( \alpha \right)\).
Trong (ABCD) kéo dài ON cắt BC tại P.
Khi đó thiết diện của hình chóp cắt bởi \(\left( \alpha \right)\) là tứ giác MNPQ.
Ta có MQ là đường trung bình của tam giác SCD \( \Rightarrow MQ\parallel CD\).
Lại có NP // CD nên MQ // CD, do đó MNPQ là hình thang.
Mà \(MN \bot \left( {ABCD} \right) \Rightarrow MN \bot NP\). Suy ra MNPQ là hình thang vuông.
Ta có: \(MQ = \dfrac{1}{2}CD = \dfrac{1}{2}a\), \(NP = CD = a\), \(MN = \dfrac{1}{2}SA = \dfrac{1}{2}a\).
Vậy \({S_{MNPQ}} = \dfrac{1}{2}.MN.\left( {MQ + NP} \right)\) \( = \dfrac{1}{2}.\dfrac{1}{2}a.\left( {\dfrac{1}{2}a + a} \right) = \dfrac{{3{a^2}}}{8}\).







