Câu hỏi
Cho tứ diện ABCD có tam giác BCD đều cạnh a, AB vuông góc với mặt phẳng (BCD), AB = 2a. M là trung điểm của đoạn AD, gọi \(\varphi \) là góc giữa CM và mặt phẳng BCD. Khi đó:
- A \(\tan \varphi = \dfrac{{\sqrt 3 }}{2}\)
- B \(\tan \varphi = \dfrac{{2\sqrt 3 }}{3}\)
- C \(\tan \varphi = \dfrac{{3\sqrt 2 }}{2}\)
- D \(\tan \varphi = \dfrac{{\sqrt 6 }}{2}\)
Phương pháp giải:
- Gọi N là trung điểm của BD. Chứng minh \(MN \bot \left( {BCD} \right)\).
- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của đường thẳng trên mặt phẳng đó.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Lời giải chi tiết:
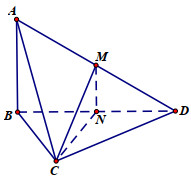
Gọi N là trung điểm của BD, ta có MN là đường trung bình của tam giác ABD nên MN // AB và \(MN = \dfrac{1}{2}AB = a.\)
Mà \(AB \bot \left( {BCD} \right)\,\,\left( {gt} \right)\) nên \(MN \bot \left( {BCD} \right)\), do đó CN là hình chiếu của CM lên (BCD)
\( \Rightarrow \angle \left( {CM;\left( {BCD} \right)} \right) = \angle \left( {CM;CN} \right) = \angle MCN = \varphi \).
Vì tam giác BCD đều cạnh a nên \(CN = \dfrac{{a\sqrt 3 }}{2}\).
Ta có: \(MN \bot \left( {BCD} \right) \Rightarrow MN \bot CN\) \( \Rightarrow \Delta CMN\) vuông tại N.
Vậy \(\tan \varphi = \tan \angle MCN = \dfrac{{MN}}{{CN}} = a:\dfrac{{a\sqrt 3 }}{2} = \dfrac{{2\sqrt 3 }}{3}\).
Chọn B.







