Câu hỏi
Cho hàm số \(y = f\left( x \right)\) liên tục trên và có đồ thị như hình vẽ sau
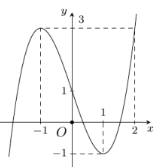
Số các giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{7^{x + 1}}} \right) - \dfrac{{{m^2} - 1}}{8} = 0\) có hai nghiệm phân biệt là:
- A \(6\)
- B \(4\)
- C \(7\)
- D \(5\)
Phương pháp giải:
- Xác định góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.
- Tính độ dài đường cao và cạnh đáy tương ứng của tam giác \(IBC\), từ đó tính diện tích tam giác.
Lời giải chi tiết:
Đặt \(t = {7^{x + 1}}\,\,\left( {t > 0} \right)\), ứng với mỗi giá trị của \(t\) cho 1 giá trị của \(x\) tương ứng, do đó để phương trình ban đầu có 2 nghiệm phân biệt thì phương trình \(f\left( t \right) - \dfrac{{{m^2} - 1}}{8} = 0 \Leftrightarrow f\left( t \right) = \dfrac{{{m^2} - 1}}{8}\) có hai nghiệm dương phân biệt.
Dựa vào đồ thị hàm số ta thấy phương trình .\(f\left( t \right) = \dfrac{{{m^2} - 1}}{8}\). có hai nghiệm dương phân biệt khi và chỉ khi \( - 1 < \dfrac{{{m^2} - 1}}{8} < 1 \Leftrightarrow - 8 < {m^2} - 1 < 8\)\( \Leftrightarrow - 7 < {m^2} < 9\) \( \Leftrightarrow - 3 < m < 3\).
Mà \(m \in \mathbb{Z}\) nên \(m \in \left\{ { - 2; - 1;0;1;2} \right\}\).
Vậy có 5 giá trị của \(m\) thỏa mãn yêu cầu bài toán.
Chọn D.







