Phương pháp giải:

Sử dụng định lí \(d \bot \left( P \right) \Rightarrow d \bot a\,\,\,\forall a \subset \left( P \right)\).

Lời giải chi tiết:

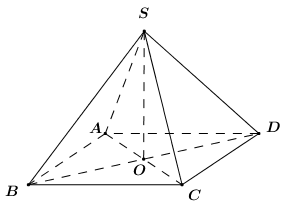
Vì \(ABCD\) là hình thoi nên \(AC \bot BD\) và \(O\) là trung điểm của \(AC,\,\,BD\).

\( \Rightarrow \) Đáp án D đúng.

Vì \(SB = SD \Rightarrow \Delta SBD\) cân tại \(S\), do đó \(SO \bot BD\) (trung tuyến đồng thời là đường cao).

Ta có: \(\left\{ \begin{array}{l}BD \bot SO\\BD \bot AC\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).

Mà \(SA,\,\,AC \subset \left( {SAC} \right)\) nên \(BD \bot SA,\,\,BD \bot SC\), suy ra các đáp án A, B đúng.

Vậy khẳng định C sai. 

Chọn C.