Phương pháp giải:

- Xác định các điểm $M,\,\,N$, chứng minh $M,\,\,N$ lần lượt là trung điểm của $SC,\,\,SD$.

- Xác định góc giữa mặt bên và mặt đáy là góc giữa hai đường thẳng lần lượt thuộc hai mặt phẳng và cùng vuông góc với giao tuyến.

- Tính đường cao $SO$ với $O$ là tâm hình vuông $ABCD$, từ đó tính ${V_{S.ABCD}}$.

- Tách ${V_{S.ABMN}} = {V_{S.ABM}} + {V_{S.AMN}}$.

- Sử dụng tỉ lệ thể tích Simpson.

Lời giải chi tiết:

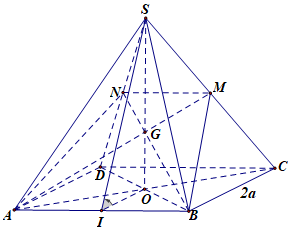
Vì $G$ là trọng tâm tam giác $SAC$ nên $AG$ cắt $SC$ tại trung điểm $M$ của $SC$, tương tự $BG$ cắt $SD$ tại trung điểm $N$ của $SD$.

Gọi $O$ là tâm của hình vuông $ABCD$ và $I$ là trung điểm của $AB$.

Ta có: $\left\{ \begin{array}{l}AB \bot OI\\AB \bot SO\end{array} \right. \Rightarrow AB \bot \left( {SOI} \right) \Rightarrow AB \bot SI$.

$\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\\\left( {ABCD} \right) \supset OI \bot AB\end{array} \right.$$\Rightarrow \angle \left( {\left( {SAB} \right);\left( {ABCD} \right)} \right) = \angle \left( {SI;OI} \right) = \angle SIO = {60^0}$.

Xét tam giác vuông $SOI$ có: $SO = OI.\tan 60^\circ  = a\sqrt 3$.

Suy ra ${V_{S.ABCD}} = \dfrac{1}{3}{S_{ABCD}}.SO = \dfrac{1}{3}4{a^2} \cdot a\sqrt 3  = \dfrac{{4{a^3}\sqrt 3 }}{3}$.

Ta có:

$\dfrac{{{V_{S.ABM}}}}{{{V_{S.ABC}}}} = \dfrac{{SA}}{{SA}} \cdot \dfrac{{SB}}{{SB}} \cdot \dfrac{{SM}}{{SC}} = \dfrac{1}{2}$ $\Rightarrow {V_{S.ABM}} = \dfrac{1}{2}.{V_{S.ABC}} = \dfrac{1}{4}{V_{S.ABCD}}$.

$\dfrac{{{V_{S.AMN}}}}{{{V_{S.ACD}}}} = \dfrac{{SA}}{{SA}} \cdot \dfrac{{SN}}{{SD}} \cdot \dfrac{{SM}}{{SC}} = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4}$ $\Rightarrow {V_{S.AMN}} = \dfrac{1}{4}.{V_{S.ACD}} = \dfrac{1}{8}{V_{S.ABCD}}$.

Vậy ${V_{S.ABMN}} = {V_{S.ABM}} + {V_{S.AMN}} = \dfrac{3}{8}{V_{S.ABCD}}$$= \dfrac{3}{8}\dfrac{{4{a^3}\sqrt 3 }}{3} = \dfrac{{{a^3}\sqrt 3 }}{2}$.

Chọn A.