Câu hỏi
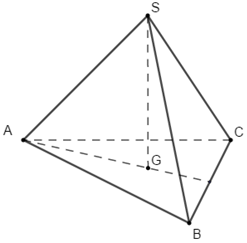
Cho hình chóp đều \(S.ABC\) có cạnh đáy bằng \(a\), chiều cao bằng \(\dfrac{{a\sqrt 3 }}{3}\). Tính góc \(\varphi \) giữa cạnh bên và mặt đáy.
- A \(\varphi = 90^\circ .\)
- B \(\varphi = 60^\circ .\)
- C \(\varphi = 30^\circ .\)
- D \(\varphi = 45^\circ .\)
Phương pháp giải:
- Gọi \(G\) là trọng tâm tam giác ABC. Khi đó \(SG \bot \left( {ABC} \right).\)
- Xác định góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
- Sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Lời giải chi tiết:
Gọi \(G\) là trọng tâm tam giác ABC. Khi đó \(SG \bot \left( {ABC} \right).\)
Khi đó ta có \(GA\) là hình chiếu của \(SA\) lên \(\left( {ABC} \right)\).
\( \Rightarrow \angle \left( {SA;\left( {ABC} \right)} \right) = \angle \left( {SA;GA} \right) = \angle SAG\).
Vì tam giác \(ABC\) đều cạnh \(a\) nên \(AG = \dfrac{2}{3}AM = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}\).
Vì \(SG \bot \left( {ABC} \right)\) nên \(SG \bot AG \Rightarrow \Delta SAG\) vuông tại \(G\).
\( \Rightarrow \tan \angle SAG = \dfrac{{SG}}{{AG}} = \dfrac{{\dfrac{{a\sqrt 3 }}{3}}}{{\dfrac{{a\sqrt 3 }}{3}}} = 1\).
Vậy \(\angle SAG = {45^0}\).
Chọn D.