Phương pháp giải:

Công thức trung tuyến: \(I{M^2} = \dfrac{{M{A^2} + M{B^2}}}{2} - \dfrac{{A{B^2}}}{4}\)

Điểm M nằm ngoài đường tròn đường kính AB có: \(M{A^2} + M{B^2} > A{B^2}\)

Điểm M là cực đại, cùng pha với hai nguồn: \(\left\{ \begin{array}{l}MA - MB = k\lambda \\MA + MB = m\lambda \end{array} \right. \Rightarrow \left\{ \begin{array}{l}MA = n\lambda \\MB = {\rm{l}}\lambda \end{array} \right.\,\,\left( {k,l,m,n \in Z} \right)\)

Lời giải chi tiết:

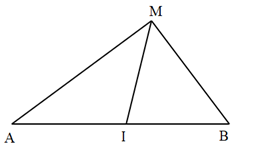
Ta có công thức trung tuyến: \(I{M^2} = \dfrac{{M{A^2} + M{B^2}}}{2} - \dfrac{{A{B^2}}}{4}\)

Vì khoảng cách \(I{M_{\min }} \Leftrightarrow {\left( {M{A^2} + M{B^2}} \right)_{\min }}\)

Do M nằm ngoài đường tròn (C), nên xét \(\Delta MAB\) ta có:

\(M{A^2} + M{B^2} > A{B^2} \Rightarrow M{A^2} + M{B^2} > {\left( {6,6\lambda } \right)^2} = 43,56{\lambda ^2}\)

Do M là cực đại cùng pha với hai nguồn → MA, MB bằng số nguyên lần bước sóng

\(\begin{array}{l}{\left( {M{A^2} + M{B^2}} \right)_{\min }} \Leftrightarrow \left[ \begin{array}{l}MA = 6;MB = 3\\MA = 3;MB = 6\end{array} \right.\\ \Rightarrow {\left( {M{A^2} + M{B^2}} \right)_{\min }} = 45{\lambda ^2} \Rightarrow I{M_{\min }} = \dfrac{{45{\lambda ^2}}}{2} - \dfrac{{{{\left( {6,6\lambda } \right)}^2}}}{4} = 3,41\lambda \end{array}\)

Chọn A.