Phương pháp giải:

- Sử dụng phương pháp hình học xác định tập hợp các điểm biểu diễn số phức \(z\).

- Tập hợp các điểm biểu diễn số phức \(z\) thỏa mãn \(\left| {z - \left( {a + bi} \right)} \right| = R\) là đường tròn tâm \(I\left( {a;b} \right)\), bán kính \(R\).

- Gọi \(M,\,\,A,\,\,B\) lần lượt là điểm biểu diễn các số phức \(z,\,\, - 1,\,\,i\). Xác định tọa độ các điểm \(M,\,\,A,\,\,B\). Đưa biểu thức \({\left| {z + 1} \right|^2} - {\left| {z - i} \right|^2}\)về biểu thức trong hình học (\(M{A^2} - M{B^2}\)).

- Xác định yếu tố cố định, yếu tố thay đổi, từ đó tìm GTLN.

Lời giải chi tiết:

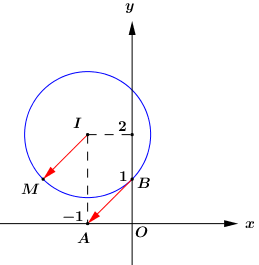
Giả sử \(z = x + yi\,\,\left( {x,y \in \mathbb{R}} \right)\) và \(M\left( {x;y} \right)\) là điểm biểu diễn của số phức \(z\) trong mặt phẳng toạ độ \(Oxy\).

Ta có : \(\left| {z + 1 - 2i} \right| = \sqrt 2  \Leftrightarrow \left| {z - \left( { - 1 + 2i} \right)} \right| = \sqrt 2 .\)

\( \Rightarrow \) Tập hợp các điểm \(M\) là đường tròn tâm \(I\left( { - 1;2} \right)\), bán kính \(R = \sqrt 2 \).

Gọi \(A\left( { - 1;0} \right),\,B\left( {0;1} \right)\) lần lượt là điểm biểu diễn các số phức \({z_1} =  - 1,\,\,{z_2} = i\).

Ta có: \(T = {\left| {\left( {x + 1} \right) + yi} \right|^2} - {\left| {x + \left( {y - 1} \right)i} \right|^2} = M{A^2} - M{B^2}.\)

  \(\begin{array}{l} = {\overrightarrow {MA} ^2} - {\overrightarrow {MB} ^2} = {\left( {\overrightarrow {MI}  + \overrightarrow {IA} } \right)^2} - {\left( {\overrightarrow {MI}  + \overrightarrow {IB} } \right)^2}\\ = M{I^2} + 2.\overrightarrow {MI} .\overrightarrow {IA}  + I{A^2} - M{I^2} - 2.\overrightarrow {MI} .\overrightarrow {IB}  - I{B^2}\\ = {2^2} - {\left( {\sqrt 2 } \right)^2} + 2.\overrightarrow {MI} .\left( {\overrightarrow {IA}  - \overrightarrow {IB} } \right)\\ = 2 + 2.\overrightarrow {MI} .\overrightarrow {AB} \\ = 2 + 2.MI.AB.{\rm{cos}}\left( {\overrightarrow {MI} ;\overrightarrow {BA} } \right)\\ \le 2 + 2MI.AB\end{array}\) 

Ta có: \(M \in \left( {I;\sqrt 2 } \right) \Rightarrow MI = \sqrt 2 \), \(AB = \sqrt {{1^2} + {1^2}}  = \sqrt 2 \).

\( \Rightarrow T \le 2 + 2.\sqrt 2 .\sqrt 2  = 6\).

Vậy \({T_{{\rm{max}}}} = 6\) khi và chỉ khi \({\rm{cos}}\left( {\overrightarrow {MI} ;\overrightarrow {BA} } \right) = 1\) hay hai vectơ \(\overrightarrow {MI} ,\,\,\overrightarrow {BA} \) cùng hướng.

Chọn D.