Phương pháp giải:

- Tính chiều cao của hình nón.

- Xác định thiết diện của mặt phẳng đi qua đỉnh của hình nón và tạo với mặt phẳng đáy của hình nón một góc bằng \({60^0}\) và mặt đáy của hình nón. Thiết diện đó là tam giác cân.

- Sử dụng định lí Pytago và tỉ số lượng giác của góc nhọn trong tam giác vuông tính chiều cao và cạnh đáy tương ứng của thiết diện.

- Tính diện tích tam giác : \({S_\Delta } = \dfrac{1}{2}a{h_a}\)

Lời giải chi tiết:

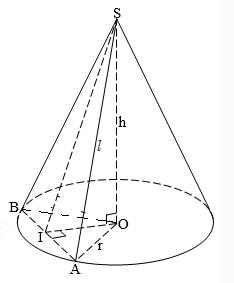
Hình nón có có đường sinh bằng \(a\) và góc ở đỉnh bằng \({90^0}\) \( \Rightarrow \angle OSA = {45^0}\).

\( \Rightarrow \Delta SOA\) vuông cân tại \(O\)\( \Rightarrow h = r = \dfrac{l}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}.\)

Thiết diện là tam giác \(SAB\) cân tại \(S\). Gọi \(I\) là trung điểm của \(AB\) ta có:

   \(SI \bot AB\) (do \(\Delta SAB\) cân tại \(S\)).

   \(OI \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung).

Ta có:

\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {OAB} \right) = AB\\\left( {SAB} \right) \supset SI \bot AB\\\left( {OAB} \right) \supset OI \bot AB\end{array} \right.\) \( \Rightarrow \angle \left( {\left( {SAB} \right);\left( {OAB} \right)} \right) = \angle \left( {SI;OI} \right) = \angle SIO = {60^0}\).

\( \Rightarrow IO = \dfrac{{SO}}{{\tan {{60}^0}}} = \dfrac{{\dfrac{a}{{\sqrt 2 }}}}{{\sqrt 3 }} = \dfrac{a}{{\sqrt 6 }},\,SI = \dfrac{{SO}}{{\sin {{60}^0}}} = \dfrac{{\dfrac{a}{{\sqrt 2 }}}}{{\dfrac{{\sqrt 3 }}{2}}} = \dfrac{{a\sqrt 6 }}{3}.\)

Áp dụng định lí Pytago trong tam giác vuông \(OAI\) ta có:

\(IA = \sqrt {O{A^2} - O{I^2}}  = \sqrt {{{\left( {\dfrac{a}{{\sqrt 2 }}} \right)}^2} - {{\left( {\dfrac{a}{{\sqrt 6 }}} \right)}^2}}  = \dfrac{a}{{\sqrt 3 }} \Rightarrow AB = \dfrac{{2a}}{{\sqrt 3 }}\)

\( \Rightarrow {S_{SAB}} = \dfrac{1}{2}.SI.AB = \dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{3}.\dfrac{{2a}}{{\sqrt 3 }} = \dfrac{{{a^2}\sqrt 2 }}{3}.\)

Chọn A.