Câu hỏi
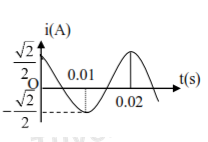
Đồ thị hình bên mô tả sự biến thiên của cường độ dòng điện xoay chiều theo thời gian. Biểu thức của cường độ dòng điện tức thời có biểu thức
- A \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t + \dfrac{\pi }{2}} \right)A.\)
- B \(i = 2cos\left( {100\pi t} \right)A.\)
- C \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A.\)
- D \(i = 1cos\left( {100\pi t} \right)A.\)
Phương pháp giải:
+ Đọc đồ thị i-t
+ Sử dụng biểu thức \(\omega = \dfrac{{2\pi }}{T}\)
+ Viết phương trình cường độ dòng điện
Lời giải chi tiết:
Từ đồ thị ta có:
+ Cường độ dòng điện cực đại: \({I_0} = \dfrac{{\sqrt 2 }}{2}A\)
+ Chu kì dao động: \(T = 0,02s\)
\( \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,02}} = 100\pi \)
+ Tại thời điểm ban đầu, dòng điện có giá trị cực đại: \( \Rightarrow {i_0} = {I_0}cos\varphi = {I_0} \Rightarrow cos\varphi = 1 \Rightarrow \varphi = 0\)
\( \Rightarrow \) Phương trình cường độ dòng điện: \(i = \dfrac{{\sqrt 2 }}{2}cos\left( {100\pi t} \right)A\)
Chọn C