 Môn Lý - Lớp 12
Môn Lý - Lớp 12
 50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng cao
50 bài tập Công suất tiêu thụ của mạch điện xoay chiều. Hệ số công suất mức độ vận dụng cao
Câu hỏi
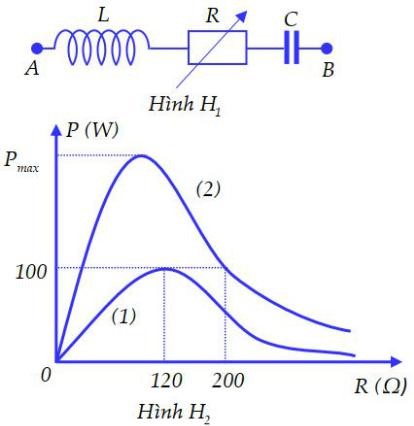
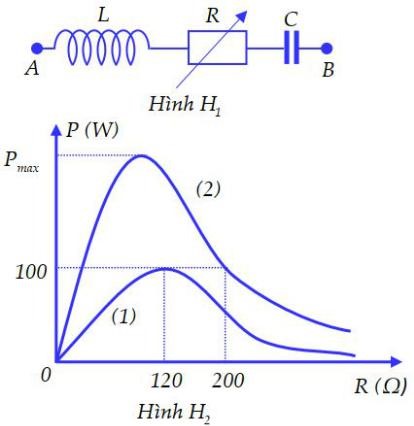
Cho đoạn mạch AB như hình H1 với L là cuộn cảm thuần, R là biến trở. Đặt vào hai đầu đoạn mạch điện áp xoay chiều có biểu thức \(u = U\sqrt 2 .\cos 2\pi ft\left( V \right)\), U không đổi nhưng f có thể thay đổi được. Hình H2 là đồ thị biểu diễn sự phụ thuộc của công suất tiêu thụ điện của mạch theo R là đường (1) khi f = f1 và là đường (2) khi f = f2. Bỏ qua điện trở của dây nối. Giá trị của Pmax gần nhất với giá trị nào sau đây?
- A 140 W
- B 260 W
- C 134 W
- D 280 W
Phương pháp giải:
Áp dụng công thức tính công suất :
\(P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}}\)
Xác định điều kiện của R để Pmax
Từ đồ thị ta thấy:
\(\left\{ \begin{array}{l}
{P_{1\max }} = 100W \Leftrightarrow {R_1} = 120\Omega \\
{P_{21}} = 100W \Leftrightarrow {R_{21}} = 200\Omega
\end{array} \right.\)
Từ đó xác định U và R20 để tìm P2max
Lời giải chi tiết:
Công thức tính công suất :
\(P = {I^2}.R = \frac{{{U^2}.R}}{{{R^2} + {{({Z_L} - {Z_C})}^2}}} = \frac{{{U^2}}}{{R + \frac{{{{({Z_L} - {Z_C})}^2}}}{R}}}\)
Áp dụng công thức Cosi cho mẫu ta có :
\(R + \frac{{{{\left( {{Z_L} - {Z_C}} \right)}^2}}}{R} \ge 2.\left| {{Z_L} - {Z_C}} \right|\)
Do đó
\({P_{\max }} = \frac{{{U^2}}}{{2\left| {{Z_L} - {Z_C}} \right|}} \Leftrightarrow R = \left| {{Z_L} - {Z_C}} \right|\)
Từ đồ thị ta thấy :
\({P_{1\max }} = 100W \Leftrightarrow \frac{{{U^2}}}{{2{R_{10}}}} = 100 \Rightarrow {U^2} = 200.{R_{10}} = 200.120 = 24000\)
Và:
\(\begin{array}{l}
{P_2} = 100W \Leftrightarrow \frac{{{U^2}.{R_2}}}{{R_2^2 + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}} = 100 \Rightarrow \frac{{24000.200}}{{{{200}^2} + {{\left( {{Z_{L2}} - {Z_{C2}}} \right)}^2}}} = 100\\
\Rightarrow {\left( {{Z_{L2}} - {Z_{C2}}} \right)^2} = 8000 \Rightarrow \left| {{Z_{L2}} - {Z_{C2}}} \right| = \sqrt {8000}
\end{array}\)
Vậy :
\({P_{2\max }} = \frac{{{U^2}}}{{2.\left| {{Z_{L2}} - {Z_{C2}}} \right|}} = \frac{{24000}}{{2.\sqrt {8000} }} \approx 134W\)
Chọn C.






