Lời giải chi tiết:

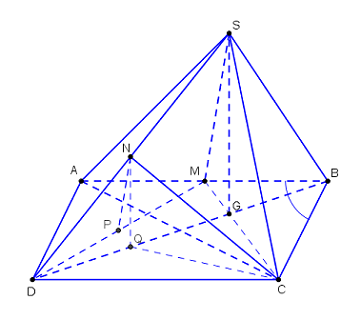
+) \({S_{ABCD}} = 2.{S_{ABC}} = 2.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^2}\sqrt 3 }}{2}\) (1)

+) Gọi P, Q lần lượt là trung điểm của MD, GD \( \Rightarrow \left\{ \begin{array}{l}NP\parallel SM \Rightarrow \left( {\widehat {SM;NC}} \right) = \left( {\widehat {NP;NC}} \right)\\NQ\parallel SG \Rightarrow NQ \bot \left( {ABCD} \right)\end{array} \right.\) .

Tính được: \(GC = QC = \dfrac{{a\sqrt 3 }}{3},\,MG = \dfrac{{a\sqrt 3 }}{6},\,DG = \dfrac{{2a\sqrt 3 }}{3}\).

Tam giác MDC vuông tại C \( \Rightarrow CP = \dfrac{1}{2}DM = \dfrac{1}{2}\sqrt {{a^2} + \dfrac{{3{a^2}}}{4}}  = \dfrac{{a\sqrt 7 }}{4}\)

Đặt \(SG = x\left( {x > 0} \right) \Rightarrow NQ = \dfrac{x}{2},\,\,SM = \sqrt {{x^2} + \dfrac{{{a^2}}}{{12}}}  \Rightarrow NP = \dfrac{1}{2}\sqrt {{x^2} + \dfrac{{{a^2}}}{{12}}} \).

Tam giác NQC vuông tại Q \( \Rightarrow NC = \sqrt {\dfrac{{{x^2}}}{4} + \dfrac{{{a^2}}}{3}} \)

Xet tam giác NPC có: \({\rm{cos}}\widehat {PNC} = \dfrac{{N{P^2} + N{C^2} - P{C^2}}}{{2.NP.NC}}\), mà \({\rm{cos}}\angle \left( {NP;NC} \right) = \dfrac{{2\sqrt {26} }}{{13}}\)

\(\begin{array}{l} \Rightarrow \left| {\dfrac{{N{P^2} + N{C^2} - P{C^2}}}{{2.NP.NC}}} \right| = \dfrac{{2\sqrt {26} }}{{13}}\\ \Leftrightarrow \left| {\dfrac{{\dfrac{1}{4}\left( {\dfrac{{{a^2}}}{{12}} + {x^2}} \right) + \left( {\dfrac{{{x^2}}}{4} + \dfrac{{{a^2}}}{3}} \right) - \dfrac{{7{{\rm{a}}^2}}}{{16}}}}{{2.\sqrt {\dfrac{1}{4}\left( {\dfrac{{{a^2}}}{{12}} + {x^2}} \right).\left( {\dfrac{{{x^2}}}{4} + \dfrac{{{a^2}}}{3}} \right)} }}} \right| = \dfrac{{2\sqrt {26} }}{{13}}\\ \Leftrightarrow \dfrac{{{{\left( {6{x^2} - {a^2}} \right)}^2}}}{{\left( {{a^2} + 12{x^2}} \right)\left( {3{x^2} + 4{a^2}} \right)}} = \dfrac{8}{{13}}\end{array}\)

\(\begin{array}{l} \Leftrightarrow 180{x^4} - 564{a^2}{x^2} - 19{a^4} = 0\\ \Leftrightarrow {x^2} = \dfrac{{19}}{6}{a^2} \Leftrightarrow x = \dfrac{{\sqrt {19} a}}{{\sqrt 6 }}\end{array}\)

\( \Rightarrow SG = \dfrac{{\sqrt {19} a}}{{\sqrt 6 }}\,\,\,\left( 2 \right)\)

Từ (1), (2) suy ra: \({V_{S.ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt {19} a}}{{\sqrt 6 }}.\dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt {38} }}{{12}}\).

Chọn D.