Câu hỏi
Một sợi dây đàn hồi có chiều dài 9a với hai đầu cố định, đang có sóng dừng. Trong các phần tử dây mà tại đó sóng tới và sóng phản xạ hình sin lệch pha nhau \( \pm \dfrac{\pi }{3} + k2\pi \) (với k là các số nguyên) thì hai phần tử dao động ngược pha cách nhau một khoảng gần nhất là a. Trên dây, khoảng cách xa nhất giữa hai phần tử dao động cùng pha với biên độ bằng một nửa biên độ của bụng sóng là
- A 8,5a
- B 8a
- C 7a
- D 7,5a
Phương pháp giải:
Biên độ của điểm tại đó sóng tới và sóng phản xạ lệch pha nhau \(\alpha :{A_M} = \sqrt {{A^2} + {A^2} + 2.A.A.cos\alpha } \)
Hai điểm dao động ngược pha khi chúng nằm trên hai bó sóng liền nhau, hoặc một điểm nằm trên bó chẵn, một điểm trên bó lẻ
Hai điểm dao động cùng pha khi chúng cùng nằm trên một bó sóng, hoặc cùng nằm trên các bó sóng cùng chẵn hoặc cùng lẻ
Biên độ của điểm cách nút sóng khoảng x: \({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right|\)
Số bó sóng: \(n = \dfrac{{2{\rm{l}}}}{\lambda }\)
Lời giải chi tiết:
Biên độ của điểm có sóng tới và sóng phản xạ lệch pha nhau \( \pm \dfrac{\pi }{3} + k2\pi \) là:
\({A_P} = \sqrt {{A^2} + {A^2} + 2.A.A.cos\left( { \pm \dfrac{\pi }{3}} \right)} = A\sqrt 3 \)
Hai điểm gần nhau nhất dao động ngược pha khi chúng đối xứng qua nút sóng \( \Rightarrow x = \dfrac{a}{2}\)
Biên độ của điểm cách nút sóng khoảng x là:
\({A_P} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| \Rightarrow A\sqrt 3 = 2A.\left| {\sin \dfrac{{2\pi .\dfrac{a}{2}}}{\lambda }} \right| \Rightarrow \lambda = 3a\)
Số bó sóng trên dây là: \(n = \dfrac{{2{\rm{l}}}}{\lambda } = \dfrac{{2.9a}}{{3a}} = 6\)
Ta có hình vẽ:
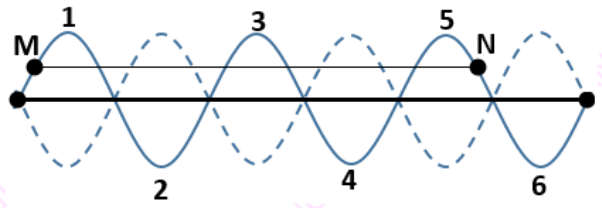
Hai điểm M, N xa nhất dao động cùng pha khi điểm M nằm trên bó sóng thứ 1, điểm N nằm trên bó sóng thứ 5
Biên độ dao động của điểm M và N là:
\({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| \Rightarrow \dfrac{{{A_{bung}}}}{2} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| \Rightarrow x = \dfrac{\lambda }{{12}}\)
Khoảng cách MN là:
\(MN = {\rm{l}} - \dfrac{\lambda }{2} - 2.x = 9a - \dfrac{{3a}}{2} - 2.\dfrac{a}{4} = 7a\)
Chọn C.







