Phương pháp giải:

Hai điểm dao động ngược pha khi chúng nằm trên hai bó sóng liền nhau, hoặc một điểm nằm trên bó chẵn, một điểm trên bó lẻ

Hai điểm dao động cùng pha khi chúng cùng nằm trên một bó sóng, hoặc cùng nằm trên các bó sóng cùng chẵn hoặc cùng lẻ

Tốc độ cực đại của phần tử dây tại bụng sóng: \({v_{\max }} = \omega .{A_{bung}}\)

Tốc độ truyền sóng: \(v = \lambda .f = \lambda .\dfrac{\omega }{{2\pi }}\)

Biên độ của điểm cách nút sóng khoảng x: \({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right|\)

Lời giải chi tiết:

Hai điểm dao động cùng pha cách nhau 65 cm khi chúng cùng nằm trên một bó sóng, hoặc cùng nằm trên các bó sóng cùng chẵn hoặc cùng lẻ

Hai điểm dao động ngược pha cách nhau 80 cm khi chúng nằm trên hai bó sóng liền nhau, hoặc một điểm nằm trên bó chẵn, một điểm trên bó lẻ

Ta có hình vẽ:

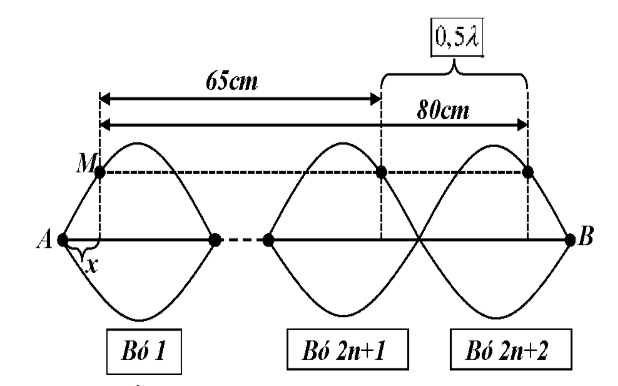
Từ hình vẽ ta thấy: \(\dfrac{\lambda }{2} = 80 - 65 \Rightarrow \lambda  = 30\,\,\left( {cm} \right)\)

Chiều dài dây là: \(AB = 80 + 2x = k\dfrac{\lambda }{2}\)

Mà \(0 < x \le \dfrac{\lambda }{4}\)

\(\begin{array}{l} \Rightarrow 0 < \dfrac{{0,5k\lambda  - 80}}{2} \le \dfrac{\lambda }{4}\\ \Rightarrow 5,3 < k \le 6,3 \Rightarrow k = 6\\ \Rightarrow 80 + 2x = 6.\dfrac{{30}}{2} \Rightarrow x = 5\,\,\left( {cm} \right)\end{array}\)

Biên độ dao động tại điểm M là:

\({A_M} = {A_{bung}}.\left| {\sin \dfrac{{2\pi x}}{\lambda }} \right| \Rightarrow 5 = {A_{bung}}.\left| {\sin \dfrac{{2\pi .5}}{{30}}} \right| \Rightarrow {A_{bung}} = \dfrac{{10}}{{\sqrt 3 }}\,\,\left( {mm} \right)\)

Tỉ số giữa tốc độ cực đại của một phần tử dây tại bụng sóng và tốc độ truyền sóng trên dây là:

\(\dfrac{{{v_{\max }}}}{v} = \dfrac{{\omega .{A_{bung}}}}{{\lambda .\dfrac{\omega }{{2\pi }}}} = \dfrac{{2\pi .{A_{bung}}}}{\lambda } = \dfrac{{2\pi .\dfrac{1}{{\sqrt 3 }}}}{{30}} = 0,12\)

Chọn A.