Phương pháp giải:

- Gọi \(I\) là trung điểm của \(BC\), chứng minh \(SI \bot \left( {ABC} \right)\).

- Kẻ \(IH \bot SC\), chứng minh \(SC \bot \left( {AHI} \right)\).

- Qua \(B\) dựng mặt phẳng song song với \(\left( {AHI} \right)\), chứng minh đó là mặt phẳng qua \(B\) và vuông góc với \(SC\).

- Sử dụng tỉ số thể tích: Cho hình chóp \(S.ABC\), các điểm \(A',\,\,B',\,\,C'\) lần lượt thuộc \(SA,\,\,SB,\,\,SC\), khi đó ta có \(\dfrac{{{V_{S.A'B'C'}}}}{{{V_{S.ABC}}}} = \dfrac{{SA'}}{{SA}}.\dfrac{{SB'}}{{SB}}.\dfrac{{SC'}}{{SC}}\).

Lời giải chi tiết:

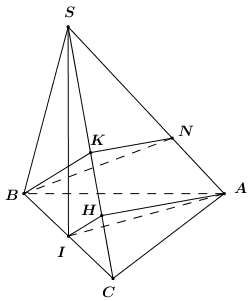
Gọi \(I\) là trung điểm của \(BC\), do tam giác \(SBC\) đều nên \(SI \bot BC\).

Ta có: \(\left\{ \begin{array}{l}\left( {SBC} \right) \bot \left( {ABC} \right)\\\left( {SBC} \right) \cap \left( {ABC} \right) = BC\\\left( {SBC} \right) \supset SI \bot BC\end{array} \right.\) \( \Rightarrow SI \bot \left( {ABC} \right)\).

Vì tam giác \(ABC\) cân tại \(A\) (gt) nên \(AI \bot BC\), lại có \(AI \bot SI\) (do \(SI \bot \left( {ABC} \right)\)) nên suy ra \(AI \bot \left( {SBC} \right)\), do đó \(AI \bot SC\).

Gọi \(K\) là trung điểm của \(SC\), do \(\Delta SBC\) đều nên \(BK \bot SC\), trong \(\left( {SBC} \right)\) kẻ \(IH\parallel BK\,\,\left( {H \in SC} \right)\) \( \Rightarrow IH \bot SC\).

Ta có: \(\left\{ \begin{array}{l}IH \bot SC\\AI \bot SC\end{array} \right. \Rightarrow SC \bot \left( {AHI} \right)\).

Trong \(\left( {SAC} \right)\) kẻ \(KN\parallel AH\,\,\left( {N \in SA} \right)\) ta có: \(\left\{ \begin{array}{l}BK\parallel IH\\KN\parallel AH\end{array} \right. \Rightarrow \left( {BKN} \right)\parallel \left( {AHI} \right)\).

Mà \(SC \bot \left( {AHI} \right) \Rightarrow SC \bot \left( {BKN} \right)\).

Do đó mặt phẳng qua \(B\) và vuông góc với \(SC\) chính là \(\left( {BKN} \right)\). Mặt phẳng \(\left( {BKN} \right)\) chia khối chóp đã cho thành hai phần. Đặt \({V_1} = {V_{S.BKN}}\), \({V_2} = {V_{BKN.ABC}}\).

Áp dụng định lí Ta-lét ta có:

\(\begin{array}{l}\dfrac{{HC}}{{HK}} = \dfrac{{IC}}{{IB}} = 1 \Rightarrow HK = HC = \dfrac{1}{2}CK = \dfrac{1}{2}SK\\ \Rightarrow \dfrac{{SK}}{{SH}} = \dfrac{2}{3} = \dfrac{{SN}}{{SA}}\\ \Rightarrow \dfrac{{{V_{SBKN}}}}{{{V_{SBCA}}}} = \dfrac{{SK}}{{SC}}.\dfrac{{SN}}{{SA}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\\ \Rightarrow {V_1} = {V_{SBKN}} = \dfrac{1}{3}{V_{SBCA}} = \dfrac{1}{3}{V_{S.ABC}}\\ \Rightarrow {V_2} = \dfrac{2}{3}{V_{S.ABC}}\end{array}\)

Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{1}{3}:\dfrac{2}{3} = \dfrac{1}{2}.\)

Chọn A.