Phương pháp giải:

- Tìm ĐKXĐ của hàm số.

- Đồ thị hàm số có 2 đường tiệm cận đứng khi và chỉ khi phương trình mẫu số = 0 có 2 nghiệm phân biệt thỏa mãn ĐKXĐ.

- Cô lập \(m\). Sử dụng phương pháp hàm số.

Lời giải chi tiết:

ĐKXĐ: \(\left\{ \begin{array}{l}0 \le x \le 6\\{x^2} - 8x + 2m > 0\end{array} \right.\)

Để đồ thị hàm số \(y = \dfrac{{20 + \sqrt {6x - {x^2}} }}{{\sqrt {{x^2} - 8x + 2m} }}\) có hai đường tiệm cận đứng thì phương trình \({x^2} - 8x + 2m = 0\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\) \( \Leftrightarrow \) Phương trình \({x^2} - 8x =  - 2m\) có hai nghiệm phân biệt thuộc đoạn \(\left[ {0;6} \right]\)(*). Xét hàm số \(f\left( x \right) = {x^2} - 8x\) ta có: \(f'\left( x \right) = 2x - 8 = 0 \Leftrightarrow x = 4.\)

Bảng biến thiên:

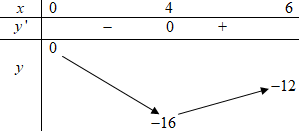
Dựa vào bảng biến thiên ta thì  \(\left( * \right) \Leftrightarrow  - 16 <  - 2m \le  - 12 \Leftrightarrow 6 \le m < 8.\)

Vậy \(m \in \left[ {6;8} \right)\).

Chọn A.