Câu hỏi
Trong thí nghiệm giao thoa với hai nguồn phát sóng giống nhau tại hai điểm A, B trên mặt nước. Khoảng cách hai nguồn là AB = 20 cm. Sóng truyền đi có bước sóng 4 cm. Trên đường thẳng x’x song song với AB, cách AB một khoảng 6 cm, gọi C là giao điểm của x’x với đường trung trực của AB. Khoảng cách ngắn nhất từ C đến điểm dao động với biên độ cực tiểu nằm trên x’x là
- A 1,17 cm
- B 1,55 cm
- C 2,15 cm
- D 2,25 cm
Phương pháp giải:
Điều kiện cực tiểu giao thoa: \({d_2} - {d_1} = \left( {k + \dfrac{1}{2}} \right)\lambda \)
Lời giải chi tiết:
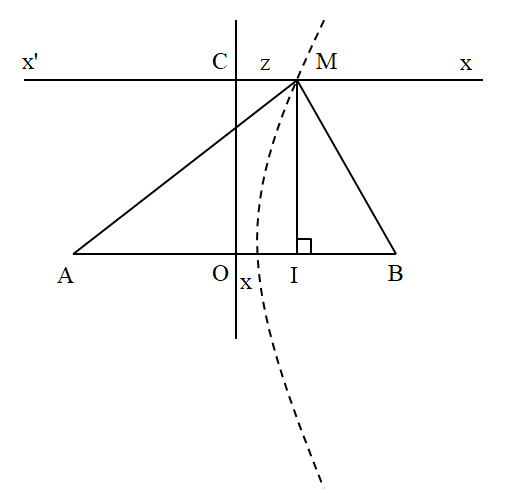
Tại M là cực tiểu gần C nhất \( \Rightarrow {k_{\min }} = 0 \Rightarrow {d_2} - {d_1} = \dfrac{\lambda }{2}\)
\(\begin{array}{l} \Rightarrow MA - MB = \sqrt {{{\left( {\dfrac{{AB}}{2} + z} \right)}^2} + O{C^2}} - \sqrt {{{\left( {\dfrac{{AB}}{2} - z} \right)}^2} + O{C^2}} = \dfrac{\lambda }{2}\\ \Rightarrow \sqrt {{{\left( {\dfrac{{20}}{2} + z} \right)}^2} + {6^2}} - \sqrt {{{\left( {\dfrac{{20}}{2} - z} \right)}^2} + {6^2}} = \dfrac{4}{2} \Rightarrow z \approx 1,17\,\,\left( {cm} \right)\end{array}\)
Chọn A.







