Phương pháp giải:

- Phân chia các khối đa diện.

- So sánh chiều cao, diện tích đáy, từ đó suy ra tỉ số thể tích các khối đa diện so với \(V = {V_{ABC.A'B'C'}}\).

Lời giải chi tiết:

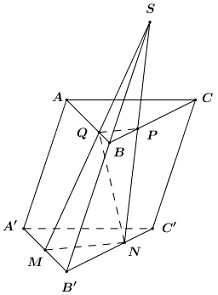
Giả sử \(AB \cap \left( {MNP} \right) = Q\), khi đó ta có: \(\left( {MNP} \right) \cap \left( {ABC} \right) = PQ\).

Mà \(\left( {MNP} \right) \cap \left( {A'B'C'} \right) = MN\), \(\left( {ABC} \right)\parallel \left( {A'B'C'} \right)\).

\( \Rightarrow MN\parallel PQ\).

Ta có: \(\)

\( \Rightarrow MQ,\,\,NP,\,\,BB'\) đồng quy tại \(S\).

Khi đó ta có: \({V_1} = {V_{B'MN.BQP}} = {V_{S.B'MN}} - {V_{S.BQP}}\).

Đặt \(V = {V_{ABC.A'B'C'}}\).

Áp dụng định lí Ta-lét ta có: \(\dfrac{{SB}}{{SB'}} = \dfrac{{BP}}{{B'N}} = \dfrac{{\dfrac{1}{3}BC}}{{\dfrac{2}{3}B'C'}} = \dfrac{1}{2}\) \( \Rightarrow B\) là trung điểm của \(SB'\).

Ta có: \(\dfrac{{{S_{B'MN}}}}{{{S_{B'A'C'}}}} = \dfrac{{B'M}}{{B'A'}}.\dfrac{{B'N}}{{B'C'}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3}\).

\(\begin{array}{l} \Rightarrow \dfrac{{{V_{S.B'MN}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{3}.\dfrac{{SB'}}{{BB'}}.\dfrac{{{S_{B'MN}}}}{{{S_{A'B'C'}}}} = \dfrac{1}{3}.2.\dfrac{1}{3} = \dfrac{2}{9}\\ \Rightarrow {V_{S.B'MN}} = \dfrac{2}{9}V\end{array}\)

Áp dụng định lí Ta-lét ta có: \(\dfrac{{BQ}}{{BA}} = \dfrac{{BQ}}{{2BM'}} = \dfrac{1}{2}.\dfrac{{SB}}{{SB'}} = \dfrac{1}{4}\)

 \( \Rightarrow \dfrac{{{S_{BQP}}}}{{{S_{ABC}}}} = \dfrac{{BQ}}{{BA}}.\dfrac{{BP}}{{BC}} = \dfrac{1}{4}.\dfrac{1}{3} = \dfrac{1}{{12}}\).

\(\begin{array}{l}\dfrac{{{V_{S.BQP}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{1}{3}.\dfrac{{SB}}{{BB'}}.\dfrac{{{S_{BQP}}}}{{{S_{ABC}}}} = \dfrac{1}{3}.1.\dfrac{1}{{12}} = \dfrac{1}{{36}}\\ \Rightarrow {V_{S.BQP}} = \dfrac{1}{{36}}V\end{array}\)

\(\begin{array}{l} \Rightarrow {V_1} = {V_{S.B'MN}} - {V_{S.BQP}} = \dfrac{2}{9}V - \dfrac{1}{{36}}V = \dfrac{7}{{36}}V\\ \Rightarrow {V_2} = V - {V_1} = \dfrac{{29}}{{36}}V\end{array}\) 

Vậy \(\dfrac{{{V_1}}}{{{V_2}}} = \dfrac{{\dfrac{7}{{36}}V}}{{\dfrac{{29}}{{36}}V}} = \dfrac{7}{{29}}.\)

Chọn B.