Câu hỏi
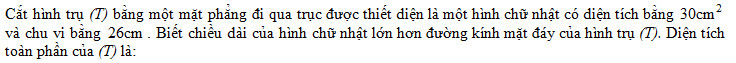
- A
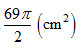
- B
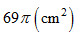
- C
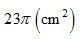
- D
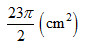
Lời giải chi tiết:
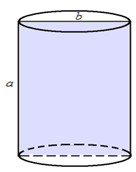
Gọi a, b (a>b) lần lượt là chiều dài của chiều rộng của thiết diện hình chữ nhật.
Ta có \(\left\{ \begin{array}{l}ab = 30\\2\left( {a + b} \right) = 26\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}ab = 30\\a + b = 13\end{array} \right.\)
Do đó a, b là nghiệm của phương trình: \({X^2} - 13X + 30 = 0 \Leftrightarrow \left[ \begin{array}{l}X = 10\\X = 3\end{array} \right.\)
Vì \(a > b \Rightarrow \left\{ \begin{array}{l}a = 10\,cm\\b = 3\,cm\end{array} \right.\)
Vì chiều dài của hình chữ nhật lớn hơn đường kính mặt đáy của hình trụ (T) nên ta có:
Chiều cao của hình trụ là:\(h = a = 10\,\,\left( {cm} \right)\)
Bán kính đáy của hình trụ là \(r = \frac{b}{2} = 1,5\,\,\left( {cm} \right)\)
Vậy diện tích toàn phần của hình trụ là: \({S_{tp}} = 2\pi rh + 2\pi {r^2} = 2\pi .1,5.10 + 2\pi {\left( {1,5} \right)^2} = \frac{{69\pi }}{2}\,\,\left( {c{m^2}} \right)\)
Chọn A.







