Câu hỏi
Cho hình chóp \(SABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a\sqrt 2 \); \(BC = a\) và \(SA = SB = SC = SD = 2a\). Gọi \(K\) là hình chiếu vuông góc của \(B\) trên \(AC\), \(H\) là hình chiếu vuông góc của \(K\) trên \(SA\). Tính cosin góc giữa đường thẳng \(SB\) và mặt phẳng \(\left( {BKH} \right)\).\(\)\(\)
- A \(\dfrac{{\sqrt 7 }}{4}\).
- B \(\dfrac{1}{{\sqrt 3 }}\).
- C \(\dfrac{{\sqrt 8 }}{5}\).
- D \(\sqrt 3 \).
Phương pháp giải:
- Góc giữa đường thẳng và mặt phẳng là góc giữa đường thẳng và hình chiếu của nó trên mặt phẳng đó.
- Sử dụng định lí Cosin trong tam giác để tính góc.
Lời giải chi tiết:
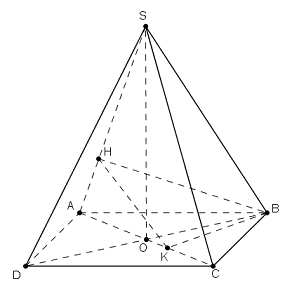
Gọi \(O = AC \cap BD\).
Hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật (tâm \(O\)), \(SA = SB = SC = SD\)\( \Rightarrow SO \bot \left( {ABCD} \right).\)
Ta có: \(\left\{ \begin{array}{l}BK \bot AC\\BK \bot SO\end{array} \right. \Rightarrow BK \bot \left( {SAC} \right) \Rightarrow BK \bot SA\).
Mà \(SA \bot HK\,\,\left( {gt} \right) \Rightarrow SA \bot \left( {BHK} \right)\).
\( \Rightarrow SH \bot \left( {BHK} \right)\) \( \Rightarrow HB\) là hình chiếu của \(SB\) lên \(\left( {BHK} \right)\).
\( \Rightarrow \angle \left( {SB;\left( {BHK} \right)} \right) = \angle \left( {SB;HB} \right) = \angle SBH\).
Xét tam giác \(SAB\) có: \({\rm{cos}}\angle ASB = \dfrac{{S{A^2} + S{B^2} - AB}}{{2.SA.SB}} = \dfrac{{4{{\rm{a}}^2} + 4{{\rm{a}}^2} - 2{{\rm{a}}^2}}}{{2.2{\rm{a}}.2{\rm{a}}}} = \dfrac{3}{4}\)
\( \Rightarrow \sin \angle ASB = \dfrac{{\sqrt 7 }}{4} \Rightarrow \cos \angle SBH = \dfrac{{\sqrt 7 }}{4}\) (Do \(\angle ASB < {90^0}\)).
Chọn: A.







