Lời giải chi tiết:

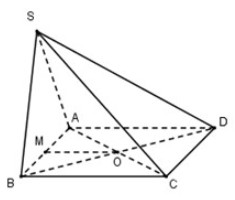
Gọi \(M\) là trung điểm của \(AB\). Vì tam giác \(SAB\) vuông tại \(S\) nên \(M\) là tâm đường tròn ngoại tiếp \(\Delta SAB\).

Gọi \(O = AC \cap BD\) \( \Rightarrow MO\) là đường trung bình của \(\Delta ABC\) \( \Rightarrow MO\parallel BC\) \( \Rightarrow MO \bot AB\).

Ta có:

\(\left\{ \begin{array}{l}\left( {SAB} \right) \bot \left( {ABCD} \right) = AB\\MO \subset \left( {ABCD} \right),\,\,MO \bot AB\end{array} \right.\) \( \Rightarrow MO \bot \left( {SAB} \right)\)  là trục của \(\left( {SAB} \right)\).

\( \Rightarrow OS = OA = OB\). Lại có \(OA = OB = OC = OD\) \( \Rightarrow OS = OA = OB = OC = OD\).

\( \Rightarrow O\) là tâm mặt cầu ngoại tiếp chóp \(S.ABCD\).

\( \Rightarrow R = OA = \dfrac{1}{2}AC = \dfrac{1}{2}a\sqrt 2  = \dfrac{{a\sqrt 2 }}{2}\).

Vậy thể tích khối cầu là: \(V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {\left( {\dfrac{{a\sqrt 2 }}{2}} \right)^3} = \dfrac{{\sqrt 2 \pi {a^3}}}{3}\).  

Chọn A.