Câu hỏi
Cho một vật dao động điều hòa với biên độ A dọc theo trục Ox và quanh gốc tọa độ O. Một đại lượng Y nào đó của vật phụ thuộc vào li độ x của vật theo đồ thị có dạng một phần của đường parabol như hình vẽ bên. Y là đại lượng nào trong số các đại lượng sau?
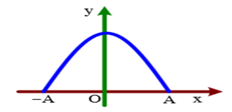
- A Thế năng
- B Động năng
- C Gia tốc
- D Lực kéo về
Phương pháp giải:
Công thức liên hệ giữa thế năng và li độ: \({{\rm{W}}_t} = \dfrac{1}{2}k{x^2}\)
Công thức liên hệ giữa động năng và li độ: \({{\rm{W}}_d} = \dfrac{1}{2}.m{v^2} = \dfrac{1}{2}.m{\omega ^2}.\left( {{A^2} - {x^2}} \right)\)
Công thức liên hệ giữa gia tốc và li độ: \(a = - {\omega ^2}x\)
Công thức liên hệ giữa lực kéo về và li độ: \(F = - k.x\)
Lời giải chi tiết:
Ta có công thức liên hệ giữa động năng và li độ là:
\({{\rm{W}}_d} = \dfrac{1}{2}.m{v^2} = \dfrac{1}{2}.m{\omega ^2}.\left( {{A^2} - {x^2}} \right) = \dfrac{1}{2}.m{\omega ^2}.{A^2} - \dfrac{1}{2}.m{\omega ^2}.{x^2}\)
Có dạng của phương trình: \(Y = A + B.{x^2}\) có đồ thị Y theo x là đường parabol
Vậy Y là động năng.
Chọn B.







