Câu hỏi
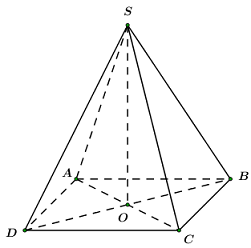
Cho hình chóp tứ giác đều \(SABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(2a\sqrt 2 .\) Khi đó góc giữa cạnh bên và mặt đáy bằng:
- A \({30^0}\)
- B \({45^0}\)
- C \({90^0}\)
- D \({60^0}\)
Phương pháp giải:
Góc giữa đường thẳng \(d\) và mặt phẳng \(\left( \alpha \right)\) là góc giữa đường thẳng \(d\) và đường thẳng \(d'\) với \(d'\) là hình chiếu của \(d\) trên \(\left( \alpha \right).\)
Lời giải chi tiết:
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)
Ta có: \(SABCD\) là hình chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right).\)
\( \Rightarrow OC\) là hình chiếu vuông góc của \(SC\) trên \(\left( {ABCD} \right).\)
\( \Rightarrow \angle \left( {SC;\,\,\left( {ABCD} \right)} \right) = \angle \left( {SC,\,\,OC} \right) = \angle SCO.\)
\(ABCD\) là hình vuông cạnh \(2a \Rightarrow AC = 2a\sqrt 2 .\)
\(\begin{array}{l} \Rightarrow OC = \dfrac{1}{2}AC = a\sqrt 2 .\\ \Rightarrow \cos \angle SCO = \dfrac{{OC}}{{SC}} = \dfrac{{a\sqrt 2 }}{{2a\sqrt 2 }} = \dfrac{1}{2}.\\ \Rightarrow \angle SCO = {60^0}.\end{array}\)
Chọn D.







