Phương pháp giải:

Cô lập \(m\) đưa bất phương trình về \(m \le f\left( x \right)\), sử dụng phương pháp hàm số tìm điều kiện.

Lời giải chi tiết:

ĐK: \(x \ge 3\).

Khi đó \(mx - \sqrt {x - 3}  \le m + 1\)\( \Leftrightarrow m\left( {x - 1} \right) \le 1 + \sqrt {x - 3} \)\( \Leftrightarrow m \le \dfrac{{1 + \sqrt {x - 3} }}{{x - 1}}\) (do \(x - 1 > 0\))

Xét \(f\left( x \right) = \dfrac{{1 + \sqrt {x - 3} }}{{x - 1}}\) trên \(\left( {3; + \infty } \right)\) có:

\(f'\left( x \right) = \dfrac{{\dfrac{1}{{2\sqrt {x - 3} }}\left( {x - 1} \right) - \left( {1 + \sqrt {x - 3} } \right)}}{{{{\left( {x - 1} \right)}^2}}}\)\( = \dfrac{{x - 1 - 2\sqrt {x - 3}  - 2\left( {x - 3} \right)}}{{{{\left( {x - 1} \right)}^2}\sqrt {x - 3} }}\)\( = \dfrac{{ - x + 5 - 2\sqrt {x - 3} }}{{{{\left( {x - 1} \right)}^2}\sqrt {x - 3} }}\)

\(f'\left( x \right) = 0 \Leftrightarrow  - x + 5 = 2\sqrt {x - 3} \)\( \Leftrightarrow \left\{ \begin{array}{l}5 - x \ge 0\\{x^2} - 10x + 25 = 4x - 12\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x \le 5\\{x^2} - 14x + 37 = 0\end{array} \right.\)

\( \Leftrightarrow \left\{ \begin{array}{l}x \le 5\\\left[ \begin{array}{l}x = 7 + 2\sqrt 3 \\x = 7 - 2\sqrt 3 \end{array} \right.\end{array} \right.\)\( \Leftrightarrow x = 7 - 2\sqrt 3  \in \left( {3; + \infty } \right)\)

Bảng biến thiên:

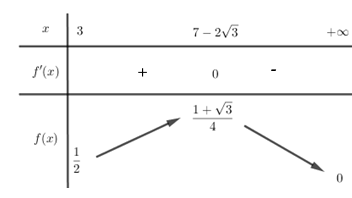
Từ BBT ta thấy, để bất phương trình vô nghiệm thì \(m > \mathop {\max }\limits_{\left[ {3; + \infty } \right)} f\left( x \right) = \dfrac{{1 + \sqrt 3 }}{4}\)

Vậy \(m \in \left( {\dfrac{{1 + \sqrt 3 }}{4}; + \infty } \right)\)  hay \(a = 1,b = 3 \Rightarrow a + b = 4\).

Chọn C.