Câu hỏi
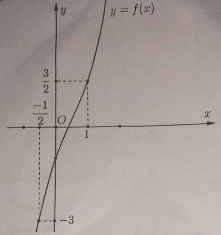
Cho hàm số \(y = f\left( x \right)\) liên tục, đồng biến trên \(\mathbb{R}\) và có đồ thị như hình vẽ dưới đây:
Phương trình \(2{x^3} - 4{x^2} + 3x - 1 = 2{x^3}\left[ {2 - f\left( x \right)} \right]\sqrt {3 - 2f\left( x \right)} \) có bao nhiêu nghiệm?
- A \(0\)
- B \(1\)
- C \(2\)
- D \(3\)
Lời giải chi tiết:
\(\begin{array}{l}\,\,\,\,\,2{x^3} - 4{x^2} + 3x - 1 = 2{x^3}\left[ {2 - f\left( x \right)} \right]\sqrt {3 - 2f\left( x \right)} \\ \Leftrightarrow 2 - \dfrac{4}{x} + \dfrac{3}{{{x^2}}} - \dfrac{1}{{{x^3}}} = \left[ {4 - 2f\left( x \right)} \right]\sqrt {3 - 2f\left( x \right)} \\ \Leftrightarrow {\left( {1 - \dfrac{1}{x}} \right)^3} + \left( {1 - \dfrac{1}{x}} \right) = {\sqrt {3 - 2f\left( x \right)} ^3} + \sqrt {3 - 2f\left( x \right)} \end{array}\)
Xét hàm số \(f\left( t \right) = {t^3} + t\) \(\left( {t \ge 0} \right)\) ta có: \(f'\left( t \right) = 3{t^2} + 1 > 0\,\,\forall t \ge 0\), do đó hàm số đồng biến trên \(\left( {0; + \infty } \right)\).
Do đó ta có: \(1 - \dfrac{1}{x} = \sqrt {3 - 2f\left( x \right)} \) \( \Leftrightarrow {\left( {1 - \dfrac{1}{x}} \right)^2} = 3 - 2f\left( x \right)\)\( \Leftrightarrow 2f\left( x \right) = - \dfrac{1}{{{x^2}}} + \dfrac{2}{x} + 2\) (*).
Đặt \(g\left( x \right) = - \dfrac{1}{{{x^2}}} + \dfrac{2}{x} + 2\) ta có \(g'\left( x \right) = \dfrac{2}{{{x^3}}} - \dfrac{2}{{{x^2}}} = - \dfrac{2}{{{x^2}}}\left( {1 - \dfrac{1}{x}} \right)\).
Do \(1 - \dfrac{1}{x} \ge 0 \Leftrightarrow - \dfrac{2}{{{x^2}}}\left( {1 - \dfrac{1}{x}} \right) \le 0\).
Do đó hàm số \(y = g\left( x \right)\) nghịch biến trên \(\left( { - \infty ;0} \right)\) và \(\left( {0; + \infty } \right)\).
Dựa vào đồ thị hàm số \(y = f\left( x \right)\) ta thấy hàm số đồng biến trên \(\mathbb{R}\).
Do đó phương trình (*) có nhiều nhất 1 nghiệm thuộc \(\left( { - \infty ;0} \right)\), 1 nghiệm thuộc \(\left( {0; + \infty } \right)\).
Dễ thấy \(2f\left( 1 \right) = 2.\dfrac{3}{2} = 3\), \(g\left( 1 \right) = 3\) \( \Rightarrow \) \(x = 1\) là nghiệm duy nhất thuộc \(\left( {0; + \infty } \right)\) của phương trình (*).
\(2f\left( { - \dfrac{1}{2}} \right) = 2.\left( { - 3} \right) = - 6\), \(g\left( {\dfrac{{ - 1}}{2}} \right) = - 6 \Rightarrow x = - \dfrac{1}{2}\) là nghiệm duy nhất thuộc \(\left( { - \infty ;0} \right)\) của phương trình (*).
Vậy phương trình ban đầu có 2 nghiệm \(x = 1,\,\,x = - \dfrac{1}{2}\).
Chọn C.