Câu hỏi
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A,\,\,B\), biết \(AB = BC = a\), \(AD = 2a\), \(SA = a\sqrt 2 \) và vuông góc với đáy. Khi đó giá trị sin của góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {SCD} \right)\) bằng:
- A \(\dfrac{{\sqrt {14} }}{7}.\)
- B \(\dfrac{{\sqrt {14} }}{{21}}.\)
- C \(\dfrac{{\sqrt {21} }}{7}.\)
- D \(\dfrac{{\sqrt {21} }}{{14}}.\)
Phương pháp giải:
- Xác định \(\alpha = \angle \left( {\left( {SBD} \right);\left( {SAD} \right)} \right)\), \(\beta = \angle \left( {\left( {SCD} \right);\left( {SAD} \right)} \right)\).
- Khi đó góc giữa \(\left( {SBD} \right)\) và \(\left( {SCD} \right)\) bằng \(\beta - \alpha \).
- Sử dụng công thức \(\sin \left( {\beta - \alpha } \right) = \sin \beta \cos \alpha - \cos \beta \sin \alpha \)
Lời giải chi tiết:
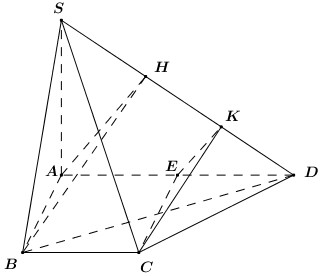
Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {SAD} \right)\).
Trong \(\left( {SAD} \right)\) kẻ \(AH \bot SD\) ta có:
\(\left\{ \begin{array}{l}AB \bot AD\\AB \bot SA\end{array} \right. \Rightarrow AB \bot \left( {SAD} \right) \Rightarrow AB \bot SD\)
\(\left\{ \begin{array}{l}AB \bot SD\\AH \bot SD\end{array} \right. \Rightarrow SD \bot \left( {ABH} \right) \Rightarrow AD \bot BH\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAD} \right) \cap \left( {SBD} \right) = SD\\\left( {SAD} \right) \supset AH \bot SD\\\left( {SBD} \right) \supset BH \bot SD\end{array} \right.\)
\( \Rightarrow \angle \left( {\left( {SAD} \right);\left( {SBD} \right)} \right) = \angle \left( {AH;BH} \right)\)
\( \Rightarrow \alpha = \angle AHB\).
Gọi \(E\) là trung điểm của \(AD\).
Kẻ \(EK \bot SD\,\,\left( {K \in SD} \right)\), tương tự ta chứng minh được \(\beta = \angle \left( {\left( {SCD} \right);\left( {SAD} \right)} \right) = \angle EKC\).
Do đó góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {SCD} \right)\) là \(\beta - \alpha \).
Ta có \(\sin \left( {\beta - \alpha } \right) = \sin \beta \cos \alpha - \cos \beta \sin \alpha \)
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(AH = \dfrac{{SA.AD}}{{\sqrt {S{A^2} + A{D^2}} }}\)\( = \dfrac{{a\sqrt 2 .2a}}{{\sqrt {2{a^2} + 4{a^2}} }} = \dfrac{{2a\sqrt 3 }}{3}\).
\( \Rightarrow EK = \dfrac{1}{2}AH = \dfrac{{a\sqrt 3 }}{3}\) (tính chất đường trung bình).
Do \(AB \bot \left( {SAD} \right) \Rightarrow AB \bot AH\) \( \Rightarrow \Delta ABH\) vuông tại \(A\).
\(\sin \beta = \dfrac{{CE}}{{CK}} = \dfrac{a}{{\sqrt {{a^2} + \dfrac{{{a^2}}}{3}} }} = \dfrac{{\sqrt 3 }}{2}\)\( \Rightarrow \cos \beta = \dfrac{1}{2}\).
Do \(CE \bot \left( {SAD} \right) \Rightarrow CE \bot EK\)\( \Rightarrow \Delta CK\) vuông tại \(E\).
\(\sin \alpha = \dfrac{{AD}}{{DH}} = \dfrac{a}{{\sqrt {{a^2} + \dfrac{{4{a^2}}}{3}} }} = \dfrac{{\sqrt {21} }}{7}\)\( \Rightarrow \cos \alpha = \dfrac{{2\sqrt 7 }}{7}\).
Vậy \(\sin \left( {\beta - \alpha } \right) = \dfrac{{\sqrt 3 }}{2}.\dfrac{{2\sqrt 7 }}{7} - \dfrac{1}{2}.\dfrac{{\sqrt {21} }}{7} = \dfrac{{\sqrt {21} }}{{14}}\).
Chọn D.







