Phương pháp giải:

Gọi \(H,E\) là trung điểm \(AB,CD\), \(K\) là hình chiếu của \(H\) lên \(SE\).

Chứng minh \(d\left( {A,\left( {SCD} \right)} \right) = d\left( {H,\left( {SCD} \right)} \right) = HK\)

Tính diện tích đáy và chiều cao suy ra thể tích.

Lời giải chi tiết:

Gọi \(H,E\) là trung điểm \(AB,CD\), \(K\) là hình chiếu của \(H\) lên \(SE\).

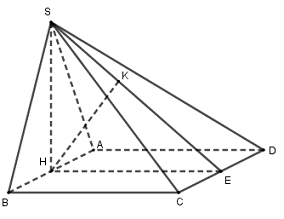
Khi đó \(SH \bot AB\), mà \(\left( {SAB} \right) \bot \left( {ABCD} \right)\) nên \(SH \bot \left( {ABCD} \right)\).

Vì \(AH//CD \subset \left( {SCD} \right)\) nên \(d\left( {A,\left( {SCD} \right)} \right) = d\left( {H,\left( {SCD} \right)} \right)\).

Dễ thấy \(CD \bot SH,CD \bot HE\) nên \(CD \bot \left( {SHE} \right) \Rightarrow CD \bot HK\)

Mà \(HK \bot SE\) nên \(HK \bot \left( {SCD} \right)\) hay \(d\left( {H,\left( {SCD} \right)} \right) = HK = a\sqrt 2 \).

Tam giác \(SHE\) vuông tại \(H\) có \(HE = AD = a\sqrt 3 ,HK = a\sqrt 2 \) nên: \(\dfrac{1}{{H{K^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{H{E^2}}}\) \( \Rightarrow \dfrac{1}{{2{a^2}}} = \dfrac{1}{{S{H^2}}} + \dfrac{1}{{3{a^2}}}\)

\( \Rightarrow \dfrac{1}{{S{H^2}}} = \dfrac{1}{{6{a^2}}} \Rightarrow SH = a\sqrt 6 \)

Diện tích hình chữ nhật \(ABCD\) là \({S_{ABCD}} = a.a\sqrt 3  = {a^2}\sqrt 3 \)

Thể tích \({V_{S.ABCD}} = \dfrac{1}{3}SH.{S_{ABCD}}\) \( = \dfrac{1}{3}.a\sqrt 6 .{a^2}\sqrt 3  = {a^3}\sqrt 2 \)

Chọn B.