Phương pháp giải:

Công thức tính thể tích khối chóp có diện tích đáy \(S\) và chiều cao \(h\) là: \(V = \dfrac{1}{3}Sh.\)

Lời giải chi tiết:

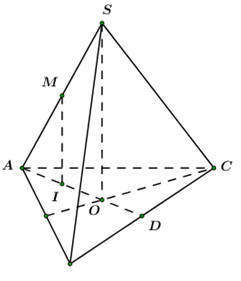
Ta có:\({S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}.\)

\(AO = \dfrac{2}{3}AD = \dfrac{2}{3}.\dfrac{{a\sqrt 3 }}{2} = \dfrac{{a\sqrt 3 }}{3}.\)

Áp dụng định lý Pitago cho \(\Delta SAO\) vuông tại \(O\) ta có:

\(SO = \sqrt {S{A^2} - A{O^2}}  = \sqrt {4{a^2} - {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {33} }}{3}.\)

Gọi \(I\) là hình chiếu vuông góc của \(M\) trên \(AO.\)

Khi đó ta có: \(MI = \dfrac{1}{2}SO\) (định lý Ta-let).

\(\begin{array}{l} \Rightarrow MI = \dfrac{{a\sqrt {35} }}{6}.\\ \Rightarrow {V_{MABC}} = \dfrac{1}{3}MI.{S_{ABC}} = \dfrac{1}{3}.\dfrac{{a\sqrt {33} }}{6}.\dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{{a^3}\sqrt {11} }}{{24}}.\end{array}\)

Chọn  D.