Câu hỏi
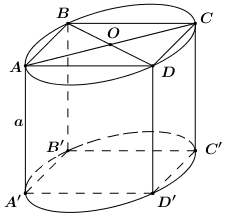
Cho hình lập phương \(ABCD.A'B'C'D'\) cạnh \(a\). Gọi \(\left( H \right)\) là hình trụ có hai đường tròn đáy lần lượt là đường tròn ngoại tiếp các hình vuông \(ABCD.A'B'C'D'\). Diện tích toàn phần của hình trụ \(\left( H \right)\) là:
- A \(\left( {2 + 2\sqrt 2 } \right)\pi {a^2}.\)
- B \(\left( {4 + \sqrt 2 } \right)\pi {a^2}.\)
- C \(\left( {2 + \sqrt 2 } \right)\pi {a^2}.\)
- D \(\left( {1 + \sqrt 2 } \right)\pi {a^2}.\)
Phương pháp giải:
Diện tích toàn phần của hình trụ có bán kính đáy \(R\), chiều cao \(h\) là: \({S_{tp}} = 2\pi R\left( {R + h} \right)\).
Lời giải chi tiết:
Gọi \(O = AC \cap BD\).
Vì \(ABCD\) là hình vuông cạnh \(a \Rightarrow AC = a\sqrt 2 \).
\( \Rightarrow OA = \frac{1}{2}AC = \frac{{a\sqrt 2 }}{2}\).
Do đó hình trụ có bán kính đáy \(R = OA = \frac{{a\sqrt 2 }}{2}\), chiều cao \(h = AA' = a\).
Diện tích toàn phần của hình trụ \(\left( H \right)\) là:
\(\begin{array}{l}{S_{tp}} = 2\pi R\left( {h + R} \right) = 2\pi .\frac{{a\sqrt 2 }}{2}\left( {a + \frac{{a\sqrt 2 }}{2}} \right)\\\,\,\,\,\,\,\, = \frac{{\sqrt 2 \left( {2 + \sqrt 2 } \right)\pi {a^2}}}{2} = \left( {1 + \sqrt 2 } \right)\pi {a^2}\end{array}\)
Chọn D.