Câu hỏi
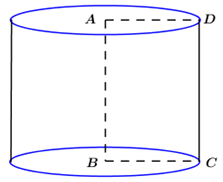
Cho \(ABCD\) là hình chữ nhật, \(AB = a,\,\,AD = b\). Quay hình chữ nhật \(ABCD\) xung quanh cạnh \(AB\) ta được một khối tròn xoay có thể tích bằng:
- A \(\frac{1}{3}\pi {a^2}b.\)
- B \(\frac{1}{3}\pi {b^2}a.\)
- C \(\pi {b^2}a.\)
- D \(\pi {a^2}b.\)
Phương pháp giải:
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được hình trụ có chiều cao \(h = AB\) và bán kính đáy \(R = AD.\)
Công thức tính thể tích của khối trụ có bán kính đáy \(R\) và chiều cao \(h:\;\;\;V = \pi {R^2}h.\)
Lời giải chi tiết:
Quay hình chữ nhật \(ABCD\) quanh cạnh \(AB\) ta được hình trụ có
chiều cao \(h = AB\) và bán kính đáy \(R = AD.\)
\( \Rightarrow V = \pi .{b^2}a = \pi a{b^2}.\)
Chọn C.
Câu hỏi trước
