Phương pháp giải:

Khảo sát hàm số đã cho trên đoạn \(\left[ { - 2;\,\,0} \right]\) để tìm \(m.\)

Lời giải chi tiết:

Xét hàm số: \(y = f\left( x \right) = 4{x^2} - 4mx + {m^2} - 2m\)

Đồ thị hàm số có tọa độ đỉnh là: \(I\left( {\frac{m}{2};\,\, - 2m} \right).\)

Lại có \(a = 4 > 0 \Rightarrow \)  hàm số nghịch biến trên \(\left( { - \infty ;\frac{m}{2}} \right)\) và đồng biến trên \(\left( {\frac{m}{2}; + \infty } \right).\)

Bảng biến thiên:

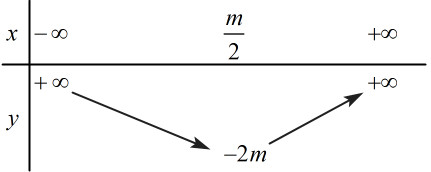
TH1: Nếu \(\frac{m}{2} \in \left[ { - 2;0} \right] \Leftrightarrow  - 2 \le \frac{m}{2} \le 0 \Leftrightarrow  - 4 \le m \le 0\) thì \(\mathop {Min}\limits_{\left[ { - 2;\,\,0} \right]} f\left( x \right) = f\left( {\frac{m}{2}} \right) =  - 2m.\)

Ta có: \({f_{\min }} = 3 \Leftrightarrow  - 2m = 3 \Leftrightarrow m =  - \frac{3}{2}\,\,\,\left( {tm} \right)\)

TH2: Nếu \(\frac{m}{2} > 0 \Leftrightarrow m > 0\) thì \(\mathop {Min}\limits_{\left[ { - 2;\,\,0} \right]} f\left( x \right) = f\left( 0 \right) = {m^2} - 2m.\)

\( \Rightarrow {f_{\min }} = 3 \Leftrightarrow {m^2} - 2m = 3 \Leftrightarrow {m^2} - 2m - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}m = 3\,\,\,\,\left( {tm} \right)\\m =  - 1\,\,\left( {ktm} \right)\end{array} \right. \Leftrightarrow m = 3\)

TH3: Nếu \(\frac{m}{2} <  - 2 \Leftrightarrow m \le  - 4\) thì  \(\mathop {Min}\limits_{\left[ { - 2;\,\,0} \right]} f\left( x \right) = f\left( { - 2} \right) = {m^2} + 6m + 16.\)

\( \Rightarrow {f_{\min }} = 3 \Leftrightarrow {m^2} + 6m + 16 = 3 \Leftrightarrow {m^2} + 6m + 13 = 0 \Rightarrow \) phương trình vô nghiệm.

Vậy \(S = \left\{ { - \frac{3}{2};3} \right\} \Rightarrow T =  - \frac{3}{2} + 3 = \frac{3}{2}.\)

Chọn D.