Câu hỏi
Cho hình nón (N) có đỉnh là S, đường tròn đáy là (O) có bán kính R=2, goc sở đỉnh của hình nón là \(\varphi = 120^\circ .\) Hình chóp đều \(S.ABCD\)có các đỉnh A,B,C,D thuộc đường tròn (O) có thể tích là
- A \(\dfrac{{8\sqrt 3 }}{3}.\)
- B \(\dfrac{{16\sqrt 3 }}{3}.\)
- C \(\dfrac{{16\sqrt 3 }}{9}.\)
- D \(\dfrac{{16}}{9}.\)
Phương pháp giải:
+ \(ABCD\) là hình vuông ngoại tiếp đường tròn đáy của hình nón. Tính độ dài cạnh hình vuông.
+ Gọi \(O\) là tâm hình vuông \(ABCD\), sử dụng tỉ số lượng giác của góc nhọn trong tam giác vuông tính \(SO\).
+ Sử dụng công thức \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\).
Lời giải chi tiết:
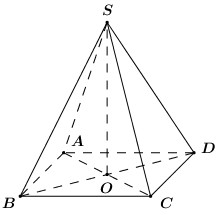
Gọi \(O\)là tâm hình vuông \(ABCD\).
Hình vuông \(ABCD\)có \(OA = OB = OC = OD = 2.\)
\( \Rightarrow AC = BD = 4 \Rightarrow AB = 2\sqrt 2 \).
Vì góc ở đỉnh của hình nón bằng \({120^0} \Rightarrow \angle BSD = {120^0} \Rightarrow \angle BSO = {60^0}.\)
Xét tam giác vuông \(SOB\) có: \(SO = OB.\cot {60^0} = 2.\dfrac{1}{{\sqrt 3 }} = \dfrac{{2\sqrt 3 }}{3}\).
Vậy \({V_{S.ABCD}} = \dfrac{1}{3}.SO.A{B^2} = \dfrac{1}{3}.\dfrac{{2\sqrt 3 }}{3}.{\left( {2\sqrt 2 } \right)^2} = \dfrac{{16\sqrt 3 }}{9}.\)
Chọn C.







