Câu hỏi
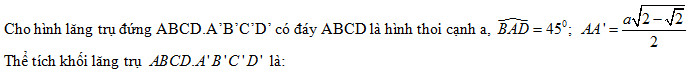
- A \({{{a^3}\sqrt {2 - \sqrt 2 } } \over {2\sqrt 2 }}\)
- B \({{{a^3}\sqrt {\sqrt 2 - 1} } \over {\sqrt 2 }}\)
- C \({{{a^3}\sqrt {\sqrt 2 - 1} } \over 4}\)
- D \({{{a^3}\sqrt {\sqrt 2 - 1} } \over 2}\)
Phương pháp giải:
+) Tính \({S_{ABD}} = \frac{1}{2}AB.AD.\sin 45\), từ đó suy ra diện tích hình thoi ABCD.
+) Tính thể tích khối lăng trụ.
Lời giải chi tiết:
Ta có: \({S_{ABD}} = \dfrac{1}{2}AB.AD.\sin 45 = \dfrac{1}{2}{a^2}\dfrac{{\sqrt 2 }}{2} = \dfrac{{{a^2}\sqrt 2 }}{4} \Rightarrow {S_{ABCD}} = 2{S_{ABD}} = \dfrac{{{a^2}\sqrt 2 }}{2}\)
\( \Rightarrow {V_{ABCD.A'B'C'D'}} = AA'.{S_{ABCD}} = {{a\sqrt {2 - \sqrt 2 } } \over 2}.{{{a^2}\sqrt 2 } \over 2} = {{{a^3}\sqrt {2 - \sqrt 2 } } \over {2\sqrt 2 }}\)
Chọn A.
Câu hỏi trước
