Phương pháp giải:

Sử dụng VTLG và công thức \(\Delta \varphi  = \omega .\Delta t\)

Áp dụng công thức tính tốc độ trung bình: \({v_{tb}} = \frac{S}{{\Delta t}}\)

Lời giải chi tiết:

Pha ban đầu của dao động: \(\varphi  =  - \frac{\pi }{4}\,\,\left( {rad} \right)\)

Chu kì dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{2\pi }} = 1\,\,\left( s \right)\)

Tại thời điểm t = 1 s → t = T

Thời điểm t = 4,625 s → \(t = 4,625T = T + 3T + \frac{{5T}}{8}\)

Trong khoảng thời gian \(\frac{{5T}}{8}\), vật quay được góc:

\(\Delta \varphi  = \omega .\Delta t = \frac{{2\pi }}{T}.\frac{{5T}}{8} = \frac{{5\pi }}{4}\,\,\left( {rad} \right)\)

Biểu diễn trên VTLG ta có:

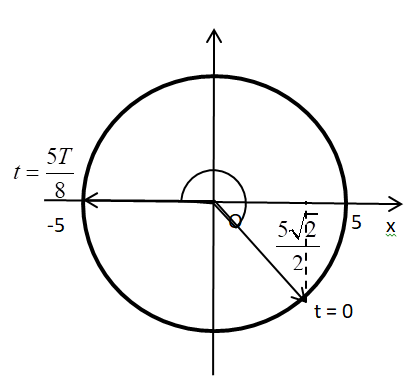
Từ VTLG, ta thấy quãng đường vật đi được là:

\(S = 3.4.5 + 2.5 + \left( {5 - \frac{{5\sqrt 2 }}{2}} \right) = 75 - \frac{{5\sqrt 2 }}{2}\,\,\left( {cm} \right)\)

Tốc độ trung bình của vật:

\({v_{tb}} = \frac{S}{{\Delta t}} = \frac{{75 - \frac{{5\sqrt 2 }}{2}}}{{4,625 - 1}} \approx 19,7\,\,\left( {cm/s} \right)\)

Chọn D.