Phương pháp giải:

Ứng dụng đường tròn lượng giác và công thức \(\Delta t = \frac{\alpha }{\omega } = \frac{{\alpha T}}{{2\pi }}\)

Lời giải chi tiết:

Chu kỳ dao động của vật: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = \frac{1}{2}s\)

Ta có: \(t = 2,125{\rm{s}} = 4.\frac{1}{2} + \frac{1}{4}.\frac{1}{2}s = 4T + \frac{T}{4}s\)

Mà trong 1 chu kỳ vật đi được quãng đường là 4 A, vậy ta chỉ cần tính quãng đường vật đi được trong thời gian \(\frac{T}{4}\)

Biểu diễn trên đường tròn lượng giác ta có:

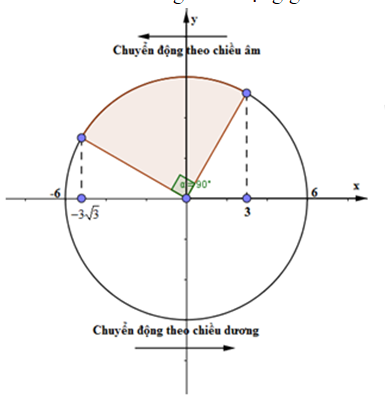
Từ VTLG, ta thấy trong khoảng thời gian \(\frac{T}{4}\) vật quét được 1 góc \(\alpha  = \Delta t.\omega  = \frac{{\frac{1}{2}}}{4}.4\pi  = \frac{\pi }{2}\)

Và vật đi từ vị trí x = 3 cm đến vị trí \(x =  - 3\sqrt 3 cm\).

Vậy quãng đường vật đi được trong thời gian t = 2,125 s là

\(s = 4.4.6 + \left| { - 3\sqrt 3  - 3} \right| = 104,196 \approx 104,2cm\)

Chọn C.