Câu hỏi
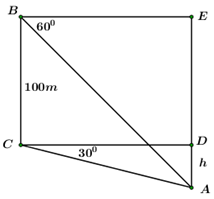
Trên quả đồi có một cái tháp cao \(100m\) . Từ đỉnh \(B\) và chân \(C\) của tháp nhìn điểm \(A\) ở chân đồi dưới các góc tương ứng bằng \({60^0}\) và \({30^0}\) so với phương nằm ngang (như hình vẽ). Chiều cao \(h\) của quả đồi là
- A \(h = 50m\)
- B \(h = 45m\)
- C \(h = 52m\)
- D \(h = 47m\)
Phương pháp giải:
Sử dụng các công thức tỉ số lượng giác của góc nhọn để làm bài toán.
Lời giải chi tiết:
Gọi \(AD = h\) là chiều cao của quả đồi.
Xét \(\Delta ACD\) vuông tại \(D\) ta có : \(\tan {30^0} = \frac{h}{{CD}} \Rightarrow h = CD.\tan {30^0} = \frac{{CD}}{{\sqrt 3 }}.\)
Xét \(\Delta ABE\) vuông tại \(E\) ta có : \(\tan {60^0} = \frac{{AE}}{{BE}} = \frac{{h + DE}}{{CD}}\)
\(\begin{array}{l} \Leftrightarrow CD.\tan {60^0} = h + BC \Leftrightarrow CD.\sqrt 3 = \frac{{CD}}{{\sqrt 3 }} + 100\\ \Leftrightarrow 3CD = CD + 100\sqrt 3 \Leftrightarrow CD = 50\sqrt 3 \,\,m.\\ \Rightarrow h = \frac{{CD}}{{\sqrt 3 }} = \frac{{50\sqrt 3 }}{{\sqrt 3 }} = 50\,\,m.\end{array}\)
Chọn A.