Lời giải chi tiết:

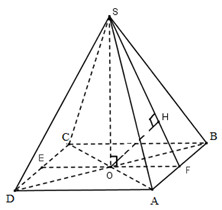
Gọi \(O = AC \cap BD\). Vì chóp S.ABCD đều nên \(SO \bot \left( {ABCD} \right)\)

Gọi E và F lần lượt là trung điểm của CD và AB

Ta có:

\(\begin{array}{l}AB//CD \Rightarrow SA \subset \left( {SAB} \right)//CD\\ \Rightarrow d\left( {CD;SA} \right) = d\left( {CD;\left( {SAB} \right)} \right) = d\left( {E;\left( {SAB} \right)} \right) = 2d\left( {O;\left( {SAB} \right)} \right) = a\sqrt 3 \\ \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = \frac{{a\sqrt 3 }}{2}\end{array}\)

Ta có:\(\left. \begin{array}{l}OF \bot AB\\SO \bot AB\,\,\left( {SO \bot \left( {ABCD} \right)} \right)\end{array} \right\} \Rightarrow AB \bot \left( {SOF} \right)\)

Trong (SOF) kẻ \(OH \bot SF\,\,\left( 1 \right)\)

Vì \(AB \bot \left( {SOF} \right) \Rightarrow AB \bot OH\,\,\left( 2 \right)\)

Từ (1) và (2) suy ra \(OH \bot \left( {SAB} \right) \Rightarrow d\left( {O;\left( {SAB} \right)} \right) = OH = \dfrac{{a\sqrt 3 }}{2}\)

Xét tam giác vuông SOF có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{S{O^2}}} + \dfrac{1}{{O{F^2}}}\)

\( \Rightarrow \dfrac{1}{{S{O^2}}} = \dfrac{1}{{O{H^2}}} - \dfrac{1}{{O{F^2}}} = \dfrac{4}{{3{a^2}}} - \dfrac{1}{{{a^2}}} = \dfrac{1}{{3{a^2}}} \Rightarrow SO = a\sqrt 3 \)

Vậy \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}} = \dfrac{1}{3}a\sqrt 3 .4{a^2} = \dfrac{{4{a^3}\sqrt 3 }}{3}\)

Chọn D.