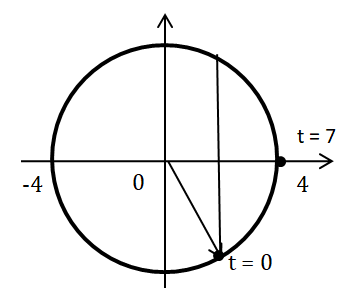Câu hỏi
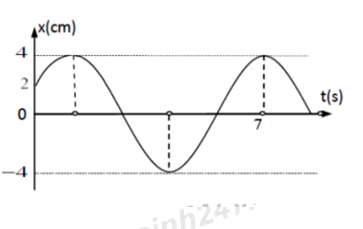
Đồ thị dao động của một chất điểm dao động điều hòa như hình vẽ. Phương trình biểu diễn sự phụ thuộc của vận tốc của vật theo thời gian là:
- A \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)\,\,\left( {cm/s} \right)\).
- B \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{6}t + \frac{{5\pi }}{6}} \right)\,\,\left( {cm/s} \right)\).
- C \(v=4\pi \cos \left( \frac{\pi }{3}t+\frac{\pi }{3} \right)\,\,\left( cm/s \right)\).
- D \(v = 4\pi \cos \left( {\frac{\pi }{6}t + \frac{\pi }{3}} \right)\,\,\left( {cm/s} \right)\).
Phương pháp giải:
Phương trình vận tốc của dao động: \(v = - A\omega \sin \left( {\omega t + \varphi } \right) = A\omega \cos \left( {\omega t + \varphi + \frac{\pi }{2}} \right)\).
Lời giải chi tiết:
Từ đồ thị, nhận xét A = 4 cm.
Tại thời điểm t = 0, vật ở li độ x = 2 cm chuyển động về biên dương → \(\varphi = - \frac{\pi }{3}\).
Tại thời điểm t = 7 s, \(\Delta \varphi = 2\pi + \frac{\pi }{3} = \frac{{7\pi }}{3} \Rightarrow \omega = \frac{{\Delta \varphi }}{{\Delta t}} = \frac{{\frac{{7\pi }}{3}}}{7} = \frac{\pi }{3}\left( {rad/s} \right)\).
Phương trình vận tốc: \(v = \frac{{4\pi }}{3}\cos \left( {\frac{\pi }{3}t + \frac{\pi }{6}} \right)\,\,\left( {cm/s} \right)\).
Chọn A.