Lời giải chi tiết:

+ Xét đáp án A: \(y = {x^4} + 2{x^2} - 2018\) có \(y' = 4{x^3} + 4x = 0 \Leftrightarrow x = 0\).

BBT:

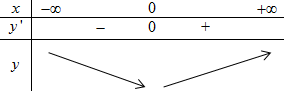
Hàm số đồng biến trên \(\left( {0; + \infty } \right)\) và nghịch biến trên \(\left( { - \infty ;0} \right)\). Loại đáp án A.

+ Xét đáp án B: \(y = \dfrac{{x + 2019}}{{x - 2018}}\) ta có \(y' = \dfrac{{ - 4037}}{{{{\left( {x - 2018} \right)}^2}}} < 0\,\,\forall x \ne 2018 \Rightarrow \) Hàm số luôn nghịch biến trên các khoảng xác định.

+ Xét đáp án C: \(y = \dfrac{{x - 2}}{{x + 2018}}\) có \(y' = \dfrac{{2020}}{{{{\left( {x + 2018} \right)}^2}}} > 0\,\,\forall x \ne  - 2018 \Rightarrow \) Hàm số luôn đồng biến trên các khoảng xác định nên loại đáp án C.

+ Xét đáp án D: \(y = {x^3} - 3x + 2019\) có \(y' = 3{x^2} - 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x =  - 1\end{array} \right.\).

BBT: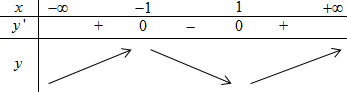

Hàm số dồng biến trên \(\left( { - \infty ; - 1} \right);\,\,\left( {1; + \infty } \right)\) và nghịch biến trên \(\left( {0;1} \right)\). Loại đáp án D.

Chọn B